Problema 525
Propuesto por Ercole Suppa, profesor titular de matemáticas y física del Liceo Scientifico “A. Einstein”, 64100 Teramo, Italia
Sea H el ortocentro del triángulo ABC. Demostrar que las circunferencias de diámetros CH y AB son ortogonales.
Alasia, C. (1900): La recente geometria del triangolo, problema 195, pag. 293
Solución de Nicola Tancredi profesor de Matemática y Física en el liceo Scientifico "G. Galilei" di Sapri (Sa), Italia
![]()
 Come è noto dalla geometria
euclidea dato un triangolo rettangolo la circonferenza che ha come diametro
l’ipotenusa ( il centro coincidente con il punto medio dell’ipotenusa stessa ) circoscrive
il triangolo.
Come è noto dalla geometria
euclidea dato un triangolo rettangolo la circonferenza che ha come diametro
l’ipotenusa ( il centro coincidente con il punto medio dell’ipotenusa stessa ) circoscrive
il triangolo.
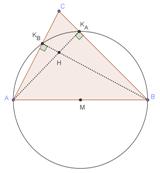
Pertanto dato un triangolo ABC
![]() La circonferenza che ha come
diametro il lato AB deve passare per i piedi delle altezze condotte dai vertici
A e da B e indicati nella Fig. 1 con KA e KB essendo retti gli angoli AKAB e AKBB.
La circonferenza che ha come
diametro il lato AB deve passare per i piedi delle altezze condotte dai vertici
A e da B e indicati nella Fig. 1 con KA e KB essendo retti gli angoli AKAB e AKBB.
![]()
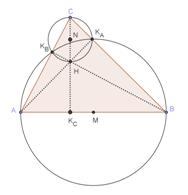 La circonferenza di
diametro CH, con H ortocentro della circonferenza ABC, dovrà passare per KA e KB essendo retti gli angoli CKAH e CKBH.
La circonferenza di
diametro CH, con H ortocentro della circonferenza ABC, dovrà passare per KA e KB essendo retti gli angoli CKAH e CKBH.
![]()
Le due circonferenze C1 e C2 aventi per diametri AB e CH si intersecano nei punti KA e KB piedi delle altezze del triangolo ABC condotte da A e da B. (Fig. 2)
Detti M e N i centri delle due circonferenze C1 e C2 per dimostrare l’ortogonalità occorre dimostrare che i gli angoli MKBN e MKAN sono retti.
Osservando la Fig. 3 abbiamo
Ø L’angolo KCCA e KCAC sono complementari essendo il triangolo AKCC rettangolo.
Ø ![]()
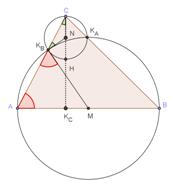 L’angolo KCCA è
congruente con l’angolo NKBC essendo angoli alla base del triangolo
isoscele KBNC di base KBC .
L’angolo KCCA è
congruente con l’angolo NKBC essendo angoli alla base del triangolo
isoscele KBNC di base KBC .
Ø L’angolo KCAC è congruente con l’angolo MKBA essendo angoli alla base del triangolo isoscele KBMA di base KBA .
Ø L’angolo MKBN è retto essendo supplementare dell’angolo retto ottenuto dalla somma di MKBA con NKBC .
Analogamente si dimostra che l’angolo MKAN è retto.
C.V.D.