Problema 526

Propuesto por Ercole Suppa, profesor titular de matemáticas y física del Liceo Scientifico “A. Einstein”, 64100 Teramo, Italia

Sean PA y QA dos segmentos isogonales respecto al ángulo A. Demostrar que las cuatro proyecciones de P y Q sobre AB y AC pertenecen a una circunferencia

Alasia, C. (1900): La recente geometria del triangolo, problema 154, pag. 289

Solución de Nicola Tancredi profesor de Matemática y Física en el liceo Scientifico "G. Galilei" di Sapri (Sa), Italia

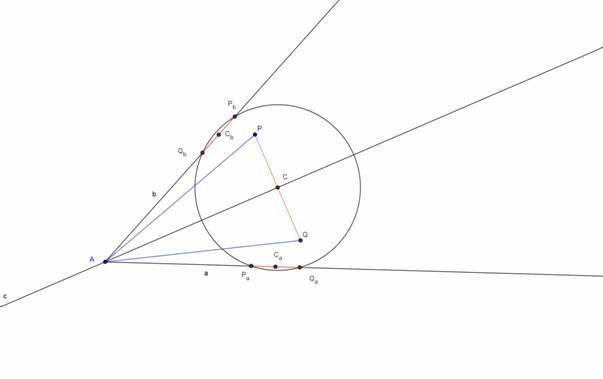
Si dicono isogonali i segmenti simmetrici alla bisettrice di un angolo ed uscenti dallo stesso vertice. Sia AP isogonale di AQ rispetto all’angolo A.

Chiamiamo P_a e Q_a  le proiezioni ortogonali dei punti P e Q sul lato a dell’angolo A e P_b e Q_b  le proiezioni ortogonali dei punti P e Q sul lato b dell’angolo A.

Dalla congruenza dei triangoli AP_bP con AQ_aQ e dei triangoli AP_aP con AQ_bQ si deduce che:

Ø       P_b è il punto simmetrico di Q_a rispetto alla bisettrice dell’angolo A.

Ø       P_a è il punto simmetrico di Q_b rispetto alla bisettrice dell’angolo A.

Tali punti simmetrici sono equidistanti da un generico punto della bisettrice in particolare da C punto medio di PQ. In formule CP_b = CQ_a  e  CP_a = CQ_b 

Dal momento che gli assi dei segmenti P_aP_b e Q_aQ_b per il teorema di Talete passeranno per il punto C ne segue che CP_a = CQ_a  e  CP_b = CQ_b  perciò

CP_a = CQ_a = CP_b = CQ_b  cioè i punti P_a ,Q_a , P_b e Q_b  appartengono alla circonferenza di centro C e raggio R = CP_a.

C.V.D.