Problema 527:
Determineu un punt en la base d’un triangle donat de forma que des d’ell es tracen perpendiculars als costats, la línia que uneix els extrems siga paral·lela a la base.
1.-Solució trigonomètrica.
2.- Solució geomètrica.
Solución de Ricard Peiró i Estruch Profesor de Matemáticas del IES "Abastos" (Valencia)
1.- Solució trigonomètrica.
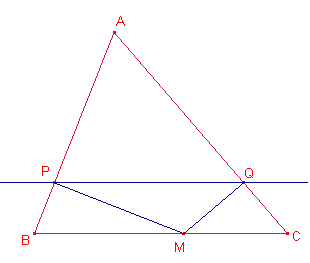
Siga
el triangle ![]() :
:
Siga
M un punt del costat ![]() . Siguen P, Q les projeccions de P i Q, sobre els costats
. Siguen P, Q les projeccions de P i Q, sobre els costats ![]() i
i ![]() , respectivament, tal que
, respectivament, tal que ![]() és paral·lel a
és paral·lel a ![]() .
.
Siga ![]() ,
, ![]() ,
, ![]() .
.
Els
triangles ![]() ,
, ![]() són semblants.
Aplicant el teorema de Tales:
són semblants.
Aplicant el teorema de Tales:
![]() (1)
(1)
Aplicant
raons trigonomètriques als triangles rectangles ![]() ,
, ![]() , respectivament:
, respectivament:
![]() (2)
(2)
![]() (3)
(3)
Dividint les expressions (2), (3):
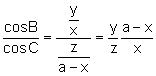 (4)
(4)
Substituint l’expressió (1) en l’expressió (4):
![]() .
.
Aplicant
el teorema del cosinus al triangle ![]() :
:
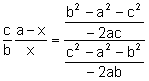 (5)
(5)
Resolent l’equació en la incògnita x:
![]() .
.
2.- Solució geomètrica.
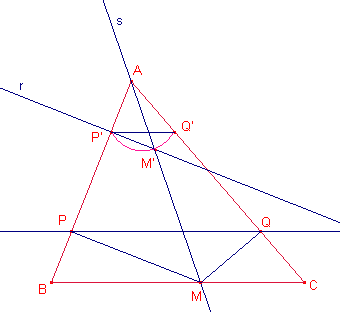
Suposem
resolt el problema siga M un punt del costat ![]() i siguen P, Q les
projeccions de P i Q, sobre els costats
i siguen P, Q les
projeccions de P i Q, sobre els costats ![]() i
i ![]() , respectivament, tal que
, respectivament, tal que ![]() és paral·lel a
és paral·lel a ![]() .
.
Notem
que ![]() . A més a més, el quadrilàter APMQ és inscriptible en una
circumferència.
. A més a més, el quadrilàter APMQ és inscriptible en una
circumferència.
Mètode de construcció.
Construïm
el quadrilàter AP’M’Q’ tal que ![]() és paral·lel a
és paral·lel a ![]() tal que
tal que ![]()
![]() perpendicular a
perpendicular a ![]() i
i ![]() , respectivament.
, respectivament.
Aquest quadrilàter AP’Q’M’ és homotètic al quadrilàter APMQ.
a) Dibuixeu el segment ![]() paral·lel a
paral·lel a ![]() .
.
b) Dibuixeu sobre el segment ![]() l’arc capaç de
l’arc capaç de ![]() .
.
c) Dibuixeu la recta r perpendicular al costat ![]() que passa per P’.
que passa per P’.
d) Feu la intersecció M’ de la recta r i l’art capaç.
e) Dibuixeu la recta s que passa pels punts A, M’
f) Feu la intersecció M de la recta s i el costat ![]() .
.
Aquest és el punt que cerquem.