Problema 527:
Determineu un punt en la base d’un triángulo donat de forma que des d’ell es tracen perpencdiculars als lados, la línia que uneix els extrems sea paraleloa a la base.
1.-Solució trigonomètrica.
2.- Solució geomètrica.
Solución de Ricard Peiró i Estruch Profesor de Matemáticas del IES "Abastos" (Valencia)
1.- Solució trigonomètrica.
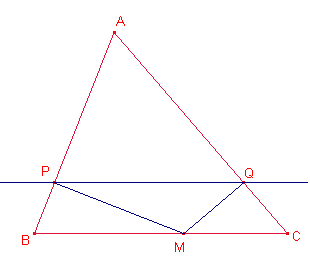
Sea el triángulo ![]() :
:
Sea M un punto del lado ![]() . Sean P, Q les proyecciones de P y Q, sobre los lados
. Sean P, Q les proyecciones de P y Q, sobre los lados ![]() y
y ![]() , respectivamente, tal que
, respectivamente, tal que ![]() es paralelo a
es paralelo a ![]() .
.
Sea ![]() ,
, ![]() ,
, ![]() .
.
Los triángulos ![]() ,
, ![]() son semejantes.
Aplicando el teorema de Tales:
son semejantes.
Aplicando el teorema de Tales:
![]() (1)
(1)
Aplicando razones trigonométricas a los triángulos rectángulos ![]() ,
, ![]() , respectivamente:
, respectivamente:
![]() (2)
(2)
![]() (3)
(3)
Dividiendo las expresiones (2), (3):
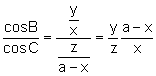 (4)
(4)
Substituyendo la expresión (1) en la expresión (4):
![]() .
.
Aplicando el teorema del coseno al triángulo ![]() :
:
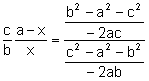 (5)
(5)
Resolviendo la ecuación en la incógnita x:
![]() .
.
2.- Solución geométrica.
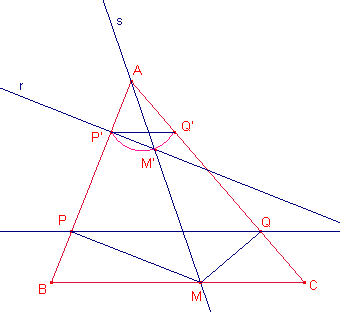
Supongamos resuelto el problema sea M un punto del lado ![]() y sean P, Q las proyecciones
de P y Q, sobre los lados
y sean P, Q las proyecciones
de P y Q, sobre los lados ![]() i
i ![]() , respectivamente, tal que
, respectivamente, tal que ![]() es paralelo a
es paralelo a ![]() .
.
Notemos que ![]() . Además, el cuadrilátero APMQ está inscrito en una circunferencia.
. Además, el cuadrilátero APMQ está inscrito en una circunferencia.
Método de construcción.
Construimos el cuadrilátero AP’M’Q’ tal que ![]() es paralelo a
es paralelo a ![]() y tal que
y tal que ![]()
![]() perpendicular a
perpendicular a ![]() y
y ![]() , respectivamente.
, respectivamente.
Este cuadrilátero AP’Q’M’ es homotético al cuadrilátero APMQ.
a) Dibujar el segmento ![]() paralelo a
paralelo a ![]() .
.
b) Dibujar sobre el segmento ![]() el arco capaz de
el arco capaz de ![]() .
.
c) Dibujar la recta r perpendicular al lado ![]() que pasa por P’.
que pasa por P’.
d) Determinar la intersección M’ de la recta r y el arco capaz.
e) Dibujar la recta s que pasa por los puntos A, M’
f) Determinar la intersección M de la
recta s y el lado ![]() .
.
Este es el punto que buscamos.