Problena 527
Encontrar un punto en
la base de un triángulo dado de forma que desde él se trazan perpendiculares a
los lados, la línea que una sus extremos sea paralela a la base. Resolver (1)
trigonométricamente, (2) geométricamente.
Carroll, L. (2005): Problemas de
almohada. Nívola. [Pillow Problems] (traducción de Guillén Rojas, y Jesús
Fernández)
Solución de Nicola Tancredi profesor
de Matemática y Física en el liceo Scientifico "G. Galilei" di Sapri
(Sa), Italia
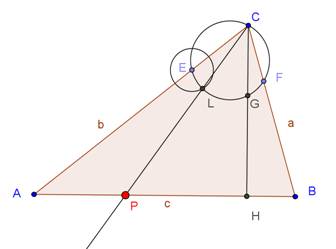 Dato il
triangolo ABC, consideriamo AB come base e siano gli angoli adiacenti alla base
acuti (per fissare le idee sia B > A), determiniamo il punto P sulla base AB
del triangolo con riga e compasso. (Vedi Fig.1)
Dato il
triangolo ABC, consideriamo AB come base e siano gli angoli adiacenti alla base
acuti (per fissare le idee sia B > A), determiniamo il punto P sulla base AB
del triangolo con riga e compasso. (Vedi Fig.1)
Tracciamo l’altezza CH che per ipotesi cadrà sul
lato AB. Tracciamo una circonferenza passante per C e che intersechi i lati CA
, CB e l’altezza CH nei punti che chiameremo E , F e G rispettivamente. Con
apertura del compasso FG puntiamo in E ed individuamo sulla circonferenza il
punto L all’interno del triangolo ABC. Tracciamo la retta passante per C e per
L che intersecherà la base AB nel punto P cercato.
Più semplicemente basta scegliere il punto P su AB
in modo tale che l’angolo ACP sia il complementare dell’angolo acuto nel
vertice B del triangolo ABC (con B>A).
Ora dimostriamo che il punto P verifica il teorema ,
cioè le sue proiezioni ortogonali sui lati AC e BC individuano una retta
parallela alla base AB.
Consideriamo il punto medio M di CP e tracciamo la
circonferenza di diametro CP. Tale circonferenza passerà per i punti vedi Fig.
2
![]()
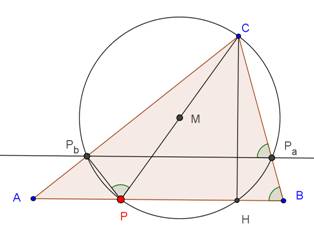 Il piede dell’altezza H ,
essendo PHC un angolo retto
Il piede dell’altezza H ,
essendo PHC un angolo retto
![]() La
proiezione ortogonale di P sul lato AC indicata con Pb , essendo PPbC
un angolo retto
La
proiezione ortogonale di P sul lato AC indicata con Pb , essendo PPbC
un angolo retto
![]() La
proiezione ortogonale di P sul lato AB indicata con Pa , essendo PPaC
un angolo retto
La
proiezione ortogonale di P sul lato AB indicata con Pa , essendo PPaC
un angolo retto
Osserviamo che
Ø L’angolo
HBC è complementare dell’angolo BCH essendo CH altezza.
Ø L’angolo
ACP è congruente all’angolo BCH per costruzione.
Ø L’angolo
PbPC è congruente all’angolo PbPaC perché
angoli alla circonferenza che insistono sulla stessa corda CPb.
Ø
L’angolo PbPC è
il complementare di PbCP essendo l’angolo PPbP retto.
Ø
L’angolo PbPC è
congruente ad HBC essendo complementari di angoli congruenti.
Ne consegue che l’angolo PbPaC
è congruente all’angolo HBC e pertanto la retta PbPa è
parallela alla base AB.
C.V.D.