Problema 527.- Encontrar un punto en la base de un triángulo dado de forma que desde él se trazan perpendiculares a los lados y la línea que une sus extremos es paralela a la base. Resolver (a) trigonométricamente (b) geométricamente

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

Supondremos la construcción pedida efectuada sobre cualquiera de los lados del triángulo ABC en caso de que éste sea acutángulo, o sobre el lado que subtiende el ángulo obtuso en caso de que éste sea obtusángulo.

(a) Trigonométricamente

Sea D el punto sobre el lado BC que estamos buscando. Sean E y F las proyecciones ortogonales de este punto sobre los lados AB y AC del triángulo, respectivamente, tal que EF sea paralelo a BC. Sean E´ y F´ los pies de las perpendiculares de los puntos E y F sobre el lado BC, respectivamente. Sea . Utilizando trigonometría elemental y el hecho de que , tenemos

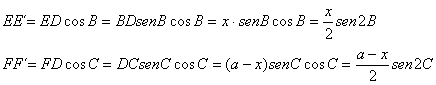
e igualando

lo que resuelve el problema.

(b) Geométricamente

En este caso construiremos el punto A´ exterior al triángulo de tal forma que  y . Unamos el punto A´ con el punto A, cortando en el punto D al lado BC. Veamos que este punto D  es el punto buscado. La razón es sencilla ya que si trazamos las perpendiculares desde D a los lados AB y AC del triángulo obteniendo respectivamente los puntos E y F, claramente se ve que los cuadriláteros ABA´C y AEDF son homotéticos, con centro de homotecia el punto A, y en consecuencia, EF es paralelo a BC.

---oooOooo---