Problema 528.-  (Propuesto por J. B. Romero Márquez, profesor colaborador de la Universidad de Valladolid).

Siendo A, B, C los ángulos de un triángulo ABC y W el ángulo de Brocard, demostrar la relación:

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva

A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triángulo. Comenzaremos recordando el problema 450 de esta misma revista que yo propuse y en cuya resolución aparece demostrado el siguiente resultado clásico entre el ángulo de Brocard y los ángulos del triángulo

                                               [1]

Por otra parte, a partir del teorema de los cosenos y una de las expresiones del área de un triángulo, es claro que

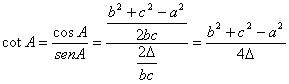                                             [2]

obteniéndose expresiones análogas para  y . Además, teniendo en cuenta la expresión trigonométrica para la tangente de la diferencia de dos ángulos, podemos obtener fácilmente la relación para las cotangentes

                             [3]

Por tanto, el enunciado del problema quedará demostrado si se cumple la siguiente identidad trigonométrica

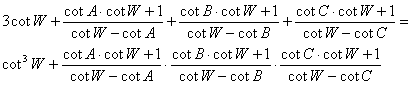              [4]

Por otra parte, es fácil ver que

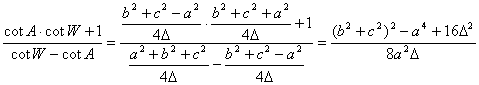
y expresiones similares para los otros dos términos. En consecuencia, sustituyendo las expresiones [1] , [2] y [3] en la expresión [4], tenemos que

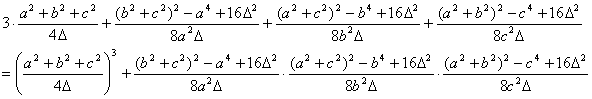
Finalmente, utilizando el teorema de Herón para el área de un triángulo en la forma , sustituyendo en la última expresión, y simplificando, se comprueba la identidad tras un trabajo analítico algo pesado, teniendo en cuenta que

y expresiones similares para los otros dos términos.

---oooOooo---

Nota: Se puede emplear algún programa de cálculo simbólico como DERIVE, MATLAB, MATHEMATICA, para verificar la última identidad. Yo la he comprobado con DERIVE 2.59.