D’entre tots els triangle de perímetre fix, determineu aquell que el girar al voltant d’un dels seus costats engendra una figura de revolució de volum màxim.
Solució Ricard Peiró:
D’entre tots els triangles de perímetre constant i base constant el d’àrea màxima és el triangle isòsceles.
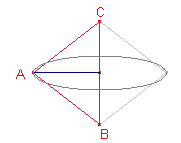
Siga a el costat desigual del triangle isòsceles.
Siga p el perímetre del triangle isòsceles.
Cadascun
dels altres dos costat mesuren: ![]() .
.
Aplicant el teorema de Pitàgores, l’altura del triangle isòsceles sobre el costat desigual és:
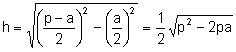 .
.
Vegem el triangle isòsceles de perímetre constant p i base a aquell que al girar al voltant del costat a dona el volum màxim.
El volum a maximitzar és:
![]() .
.
![]() .
.
![]() .
.
Aquesta funció és una paràbola convexa el màxim s’assoleix en el vèrtex:
![]() .
.
En
aquest cas, ![]() , els costats iguals mesuren cadascun,
, els costats iguals mesuren cadascun, ![]() i el volum màxim és:
i el volum màxim és:
![]() .
.