De entre todos los triángulos de perímetro fijo, determinar aquel que al girar alrededor de uno de sus lados engendra una figura de revolución de volumen máximo.
Vicario, V. (2009). Comunicación personal
Solución Ricard Peiró:
De entre todos los triángulos de perímetro constante y base constante el de área màxima es el triángulo isósceles.
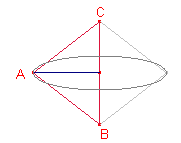
Sea a el lado desigual del triángulo isósceles.
Sea p el perímetro del triángulo isósceles.
Cada uno de los otros dos lado miden: ![]() .
.
Aplicando el teorema de Pitágoras, la altura del triángulo isósceles sobre el lado desigual es:
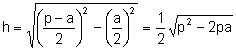 .
.
Veamos el triángulo isósceles de perímetro constante p y base a aquel que al girar alrededor del lado a tiene el volumen máximo.
El volumen a maximizar es:
![]() .
.
![]() .
.
![]() .
.
Esta función es una parábola convexa el máximo se alcanza en el vértice:
![]() .
.
En este caso, ![]() , los lados iguales miden cada uno,
, los lados iguales miden cada uno, ![]() y el volumen máximo es:
y el volumen máximo es:
![]() .
.