Problema 530
Siga ![]() un triangle acutangle.
Es dibuixen tres circumferències de diàmetres les altures. En cada una d’elles
es traça la corda perpendicular pel ortocentre a l’altura corresponent.
Demostreu que les tres cordes obtingudes tenen la mateixa longitud.
un triangle acutangle.
Es dibuixen tres circumferències de diàmetres les altures. En cada una d’elles
es traça la corda perpendicular pel ortocentre a l’altura corresponent.
Demostreu que les tres cordes obtingudes tenen la mateixa longitud.
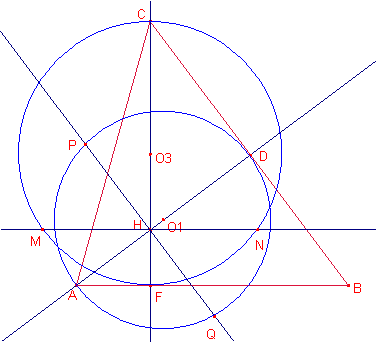 Solució de
Ricard Peiró:
Solució de
Ricard Peiró:
Siga
H l’ortocentre del triangle ![]() .
.
Siga
la circumferència de diàmetre l’altura ![]()
Siga
la recta perpendicular al diàmetre ![]() que passa per H que
talla la circumferència anterior en els punts P, Q.
que passa per H que
talla la circumferència anterior en els punts P, Q.
Notem
que ![]() .
.
Aplicant la potència del punt H respecte a aquesta circumferència:
![]() .
.
![]() .
.
Siga
la circumferència de diàmetre l’altura ![]()
Siga
la recta perpendicular al diàmetre ![]() que passa per H que
talla la circumferència anterior en els punts M, N.
que passa per H que
talla la circumferència anterior en els punts M, N.
Notem
que ![]() .
.
Aplicant la potència del punt H respecte a aquesta circumferència:
![]() .
.
![]() .
.
Volem
demostrar que ![]() .
.
Seria
suficient demostrar que ![]() .
.
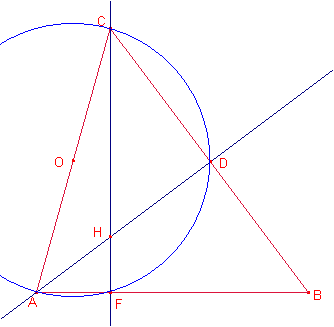
Considerem
la circumferència de diàmetre ![]() .
.
Notem que els punts D i F pertanyen a la circumferència.
Aplicant la potència de H respecte d’aquesta circumferència:
![]() .
.
Amb la tercera circumferència del problema obtindríem el mateix resultat.