Problema 530
B.4186. Sea ABC un triángulo acutángulo. Se trazan tres circunferencias de diámetros las alturas. En cada una de ellas se traza la cuerda perpendicular por el ortocentro a la altura correspondiente. Demostrar que las tres cuerdas obtenidas tienen la misma longitud.
enunciado actualizado el 2 de noviembre
Komal (2009). Mayo
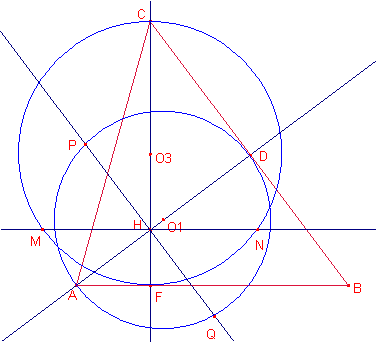 Solución de Ricard Peiró:
Solución de Ricard Peiró:
Sea H l’ortocentro del triángulo ![]() .
.
Sea la circunferencia de diámetro la altura ![]()
Sea la recta perpendicular al diámetro ![]() que pasa por H que corta
la circunferencia anterior en los puntos P, Q.
que pasa por H que corta
la circunferencia anterior en los puntos P, Q.
Notemos que ![]() .
.
Aplicando la potencia del punto H respecto a esta circunferencia:
![]() .
.
![]() .
.
Sea la circunferencia de diámetro la altura ![]()
Sea la recta perpendicular al diámetro ![]() que pasa por H que corta
la circunferencia anterior en los puntos M, N.
que pasa por H que corta
la circunferencia anterior en los puntos M, N.
Notemos que ![]() .
.
Aplicando la potencia del punto H respecto a esta circunferencia:
![]() .
.
![]() .
.
Queremos demostrar que ![]() .
.
Sería suficiente demostrar que ![]() .
.
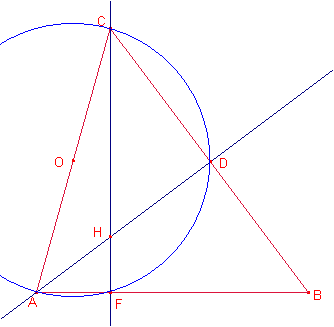
Consideremos la circunferencia de diámetro ![]() .
.
Notemos que los puntos D y F pertenecen a la circunferencia.
Aplicando la potencia de H respecto de esta circunferencia:
![]() .
.
Con la tercera circunferencia del problema obtendríamos el mismo resultado.