Problena 530

B.4186. Sea ABC un triángulo isósceles. Se trazan tres circunferencias de diámetros las alturas. En cada una de ellas se traza la cuerda perpendicular por el ortocentro a la altura correspondiente. Demostrar que las tres cuerdas obtenidas tienen la misma longitud.

Komal (2009). Mayo

Solución de Nicola Tancredi profesor de Matemática y Física en el liceo Scientifico "G. Galilei" di Sapri (Sa), Italia

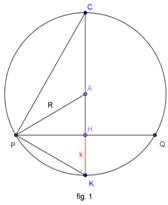
Osservazione  1

Data una circonferenza di raggio R (fig. 1) . Applicando il secondo teorema di Euclide è immediato verificare che la corda PQ ortogonale al diametro 2R e che lo divide in due parti di lunghezza k e (2R-k) sarà pari a  .

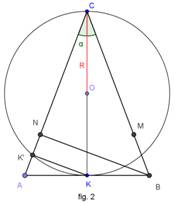
Osservazione  2

Dato un triangolo isoscele (fig. 2). Detto a l’angolo che l’altezza 2R relativa alla base forma con entrambi i lati obliqui avremo che l’altezza relativa ad uno dei lati obliqui è pari a  essendo   con     corda della semicirconferenza di diametro CK = 2 R parallela a .  

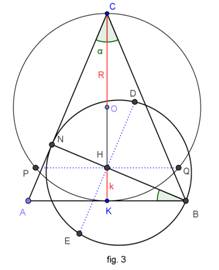
DIMOSTRAZIONE   DEL  TEOREMA

Dato il triangolo isoscele ABC di base AB. Sia H il suo ortocentro, sia  la distanza di H dalla base AB e sia a l’angolo che l’altezza 2R relativa alla base AB forma con entrambi i lati obliqui (fig. 3). Da semplici considerazioni trigonometriche segue che

      .

Inoltre essendo  avremo che

     

Dall’ osservazione 1 segue che la corda della circonferenza di diametro CK = 2R ortogonale ad essa e passante per H sarà   .

Analogamente la lunghezza della corda relativa alla circonferenza di diametro   ortogonale al relativo diametro e passante per H sarà pari a

 .

Da ciò segue che  . Per simmetria sarà verificata l’analoga relazione relativa all’altezza  .

C.V.D.