Problema 530.- Sea ABC un triángulo acutángulo. Se trazan tres circunferencias de diámetros las alturas. En cada una de ellas se traza la cuerda perpendicular por el ortocentro a la altura correspondiente. Demostrar que las tres cuerdas obtenidas tienen la misma longitud.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo de la resolución del problema emplearemos la notación habitual en la geometría del triángulo. Sea D el pie de la altura trazada desde el vértice A del triángulo sobre el lado BC. Sea H el ortocentro del triángulo (que será un punto interior al mismo, puesto que es acutángulo) y sean  A´ y  A´´ los extremos de la cuerda perpendicular al diámetro AD  pasando por el ortocentro H. Por potencia del punto H respecto de la circunferencia así construida, tenemos que

                                  [1]

Por otra parte, es inmediato ver, aplicando relaciones trigonométricas elementales y el teorema de los senos generalizado al triángulo ABC que se tiene

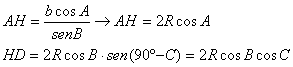
y relaciones similares para los otros segmentos. Además, sabemos que los triángulos AA´D  y AA´´D son rectángulos puesto que los ángulos en A´ y A´´ están inscritos en una misma circunferencia abarcando un diámetro de la misma. Por tanto, en virtud del teorema de la altura tenemos que

con lo que A´H  y A´´H  son segmentos de la misma longitud, cumpliéndose al aplicar [1] la relación

que, obviamente, es constante para cada triángulo elegido ABC. De forma análoga se demuestra esta igualdad para las cuerdas B´B´´ y C´C´´.

---oooOooo---