Problena 531

La circunferencia circunscrita a un triángulo biseca al segmento que une el incentro con cualquiera de los excentros de dicho triángulo.

Instituto de Ciencias y Humanidades (2005): Geometría, una visión de la planimetría, Lumbreras Editores. Lima Perú. (pag 408)

DIMOSTRAZIONE

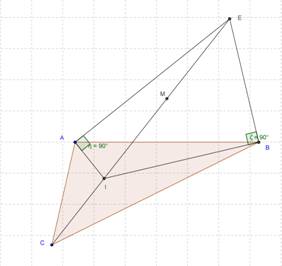Dato il triangolo ABC fissiamo la nostra attenzione sul lato AB e sull’excentro della circonferenza tangente al lato AB. Lo stesso ragionamento si potrà fare per gli altri due lati.

Costruiamo le tre bisettrici che individuano l’incentro I del triangolo ABC. Sulla bisettrice dell’angolo in C dovrà trovarsi oltre all’incentro I del triangolo ABC anche l’excentro della circonferenza tangente al lato AB. Tale punto E  si ottiene intersecando tale bisettrice con le bisettrici degli angoli esterni agli altri due angoli del triangolo ABC chiamati a e b .

Osserviamo che sia l’angolo  che   sono retti poiché la bisettrice dell’angolo di un triangolo e la bisettrice del corrispondente angolo esterno sono ortogonali. Ne consegue che il quadrilatero AIBE è ciclico e la circonferenza che lo circoscrive avrà il centro nel punto medio del segmento IE  indicato con M.

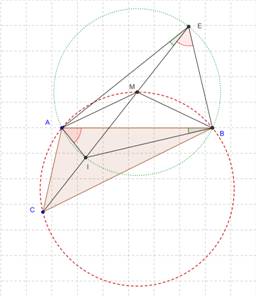Per dimostrare il teorema basta far vedere che tale punto M appartiene alla circonferenza che circoscrive il triangolo ABC e cioè che anche il quadrilatero ACBM è ciclico.

Tale proprietà segue dalle seguenti osservazioni:

    l’angolo  è congruente all’angolo   essendo angoli alla circonferenza che insistono  sullo stesso arco AI.

    l’angolo  è congruente all’angolo  essendo angoli alla circonferenza che insistono sullo stesso arco IB.

    l’angolo  è il doppio dell’angolo  essendo l’uno l’angolo al centro ed l’altro un angolo alla circonferenza che insistono sullo stesso arco AB. Pertanto .

Da ciò segue che la somma degli angoli  e  è pari a  pertanto il quadrilatero ACBM è ciclico

C.V.D.