Problema 532.- (Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva)

Sea ABC un triángulo con y M el punto medio de AB. Demostrar que existe un punto P del segmento CM de modo que las bisectrices interiores de los ángulos y se cortan en un punto Q de CM.

Nota: El propósito de este problema de existencia surge al estudiar el problema 57 del excelente libro CIEN PROBLEMAS DE MATEMÁTICAS: Combinatoria, Álgebra, Geometría; de D. F. Bellot Rosado y Mª. Asunción López Chamorro, (Instituto de Ciencias de la Educación, Universidad de Valladolid, 1992), con enunciado literal:

Problema 57: “Sea ABC un triángulo () con el ángulo agudo dado, y M el punto medio de AB. Se elige el punto P del segmento CM de modo que las bisectrices de los ángulos y se corten en un punto Q de CM. Hallar los ángulos y ”.

(Olimpiada de Bulgaria, 1985; G. Ganchev)

En la resolución de este problema 57, en dicho libro aparecen las soluciones correctas , y , pero está incompleto ya que no se demuestra previamente que tal punto P exista. Por tanto, básicamente, este es el objeto de nuestro problema.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

Para nuestra demostración de existencia, emplearemos algunas propiedades relativas a la continuidad de funciones reales de variable real, propiedades y teoremas geométricos elementales, y la notación habitual en la geometría del triángulo.

Consideremos inicialmente que el punto P del segmento CM coincide con el punto M. Sea x la longitud medida desde P del segmento más cercano a dicho punto y que genera el corte de la bisectriz interior del ángulo A con el segmento CM (que obviamente es la mediana que parte de C). En virtud del teorema de las bisectrices interiores tenemos que

De forma análoga, sea y la longitud medida desde P del segmento más cercano a dicho punto y que genera ahora la bisectriz interior que parte del ángulo B con el segmento CM. De nuevo, utilizando el mismo teorema, tenemos que

y, en consecuencia, es claro que si P coincide con M, claramente tenemos .

Situemos ahora P, precisamente en el baricentro G del triángulo dado. Denotando análogamente a x, y, pero medidos ahora a partir de G, y aplicando de nuevo el teorema de las bisectrices interiores, tenemos que

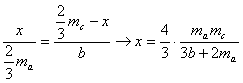
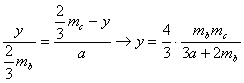
y, ahora es claro que , puesto que

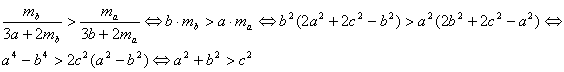
donde la última desigualdad es, obviamente cierta, a partir de las hipótesis del problema y en la que se han empleado las conocidas fórmulas de Apolonio (que se pueden deducir fácilmente) para las longitudes de las medianas en función de los lados de un triángulo

Puesto que la desigualdad entre x e y cambia cuando P coincide con M o con el baricentro G, se deduce, a partir de la continuidad de las funciones de variable real que existe un punto intermedio entre estos dos puntos M y G en el que se produce el corte de las dos bisectrices interiores que daba por supuesto el problema ya comentado.