Problema 533.- (Propuesto por J. B. Romero Márquez, profesor colaborador de la Universidad de Valladolid). Dedicado a Jack Garfunkel.

Sea ABC un triángulo acutángulo de lados a, b, c; s, R, r  semiperímetro, radio de la circunferencia circunscrita e inscrita, al triángulo, respectivamente, , ,  las medianas, , ,  las alturas correspondientes a los lados a, b, c, respectivamente. Probar que:

                                   (a)

                                   (b)

                                   (c)

                                   (d)

                                   (e)

alcanzándose la igualdad en estas desigualdades si el triángulo ABC es equilátero.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo de la resolución del problema emplearemos la notación habitual en la geometría del triángulo. Pasemos a demostrar cada una de las desigualdades. Para algunas necesitaremos lemas previos que nos facilitarán las demostraciones de las mismas.

(a) La desigualdad dada, teniendo en cuenta la conocida fórmula de Euler  se reduce a

que es cierta, ya que la última desigualdad es la famosa desigualdad de Euler del triángulo. Observemos que la desigualdad sirve para todo tipo de triángulos, no necesariamente acutángulos. La igualdad claramente se da si y sólo si el triángulo es equilátero, es decir si y sólo si .

(b) Para demostrar la desigualdad demostraremos previamente un lema

Lema 1: “En todo triángulo ABC se tiene que ”.

Demostración: Basta con emplear la desigualdad entre las medias aritmética y geométrica, la desigualdad de Euler  y la conocida desigualdad  (que se demuestra a partir de la desigualdad de Jensen) para obtener

                                                                                                                      ■

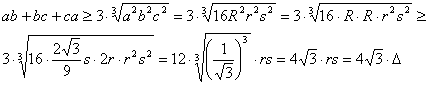
De esta forma, centrándonos en la desigualdad propuesta, empleando la fórmula de Euler en la forma , etc., y el lema anterior, obtenemos

De nuevo, la desigualdad es cierta para todo tipo de triángulo, no necesariamente acutángulo. La igualdad se da si y sólo si , es decir, si y sólo si el triángulo es equilátero.

Nota: La desigualdad  es una mejora a la famosa desigualdad de Weitzenböck

(c) Para demostrar esta desigualdad, aplicaremos la suposición de que nuestro triángulo es acutángulo. Demostraremos previamente un lema

Lema 2: “En todo triángulo acutángulo se tiene  ”.

Demostración: Basta observar que el circuncentro O de nuestro triángulo acutángulo ABC es interior al mismo, y que si denominamos por x, y, z los segmentos que unen al mismo con los puntos medios de cada uno de los lados, por la desigualdad triangular, tenemos claramente que

donde hemos aplicado el conocido teorema de Carnot que establece la identidad . [1] ■

Utilizando ahora la desigualdad entre las medias aritmética y geométrica tenemos

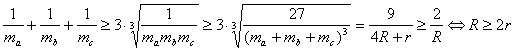
donde hemos empleado la desigualdad  y el lema 2 anterior. La igualdad, de nuevo, claramente se da si y sólo si el triángulo es equilátero.

(d) Para demostrar esta desigualdad emplearemos varios lemas que demostramos a continuación.

Lema 3: “Sea ABC un triángulo acutángulo y sea  el ángulo formado por  y , es decir, la mediana y la bisectriz interior que parten del vértice A. Entonces se tiene  ”.

Demostración: Basta observar que es bien conocido que si prolongamos la bisectriz interior que parte del vértice A, se intersecará sobre la circunferencia circunscrita al triángulo ABC con la mediatriz del lado BC, en un punto digamos A´. El triángulo AOA´ es claramente isósceles y además también es claro que , y en consecuencia, . Por tanto, se cumple que , lo que demuestra el lema.  ■

Lema 4: “En todo triángulo acutángulo ABC se tiene que  ”.

Demostración: Basta con tener en cuenta la caracterización de la demostración del lema anterior y observar que claramente .  ■

Lema 5: “En todo triángulo acutángulo ABC si  es el ángulo formado por la mediana y la bisectriz interior que parten del vértice A, tenemos que ”.[2]

Demostración: Sea  el ángulo formado por la mediana y la bisectriz interior que parten del vértice A. Completemos el triángulo ABC formando un paralelogramo ABA´C. En el triángulo AA´C se tiene claramente que

Aplicando el teorema de los senos generalizado, tenemos

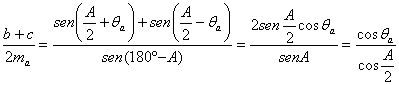
y de esta igualdad se sigue que, y por la conocida expresión , y la conocida expresión  llegamos a

     ■

Centrándonos ahora en nuestra desigualdad, denotando , ,  y con los lemas 3, 4 y 5 es claro que

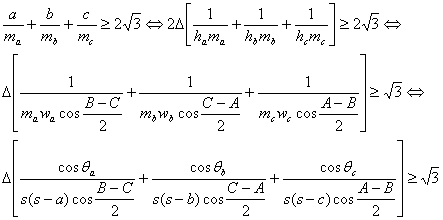
Puesto que , etc., la desigualdad anterior es cierta, ya que también lo es la siguiente cadena de desigualdades equivalentes

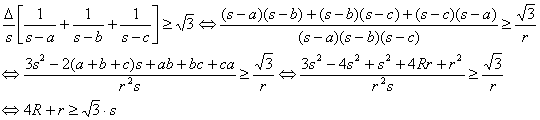
donde hemos empleado la fórmula de Herón , la conocida identidad  y la desigualdad  que es equivalente a la famosa desigualdad de Finsler-Hadwiger

cuya demostración de equivalencia aparece en mi artículo EXTRA 500 de esta misma revista. La igualdad se da claramente si el triángulo es equilátero ya que entonces todas las alturas del triángulo coincidirían con sus respectivas medianas.

(e) Para la demostración de esta desigualdad, haciendo uso de los lemas 3, 4 y 5, tenemos que

Por otra parte, como , etc., es claro que la desigualdad anterior es cierta, ya que también lo es la siguiente identidad

            La igualdad, de nuevo, claramente se da si y sólo si el triángulo es equilátero.

Nota: Aunque acabemos de demostrar que siendo ABC es un triángulo acutángulo se cumple la desigualdad , es importante observar que en sentido inverso se cumple esta otra , y cuya demostración es muy sencilla teniendo en cuenta el lema de Lau anteriormente mencionado y las caracterizaciones de los lemas, teniéndose entonces que

---oooOooo---