Problema 534.- (Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva)

Sea ABC un triángulo y K su simediano, conocido también por punto de Lemoine-Grebe del mismo. Si denota la suma de las distancias del punto simediano a los lados del triángulo, demostrar que , donde r es el radio de la circunferencia inscrita al mismo.

Nota: Este problema pretende continuar y profundizar con la línea relativa a los problemas 420 y 506 que propuso el mismo proponente en esta revista.

Resolución: Vicente Vicario García, I.E.S. El Sur, Huelva

A lo largo de la resolución del problema emplearemos la notación habitual en la geometría del triángulo. Necesitaremos dos lemas que demostramos a continuación:

Lema 1: “En todo triángulo se tiene que  ”.

Demostración: Basta con utilizar la fórmula de Herón, y la conocida relación de Euler  , para obtener después de evidentes simplificaciones

■

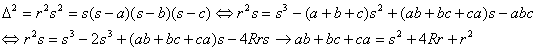Lema 2: “Sea K el simediano de un triángulo ABC y A´ el pie de la simediana que parte del vértice A sobre el lado BC. Entonces tenemos que”.

Demostración: Sean A´, B´, y C´ los pies de las simedianas que parten de los vértices A, B, C del triángulo ABC, respectivamente. A partir del conocido teorema de Van Aubel para cevianas concurrentes, tenemos que

y a partir, del teorema de las simedianas o teorema de Steiner, tenemos las relaciones

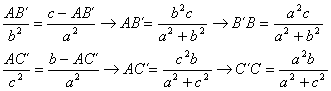
Aplicando el mencionado teorema de Van Aubel, tenemos entonces que

llegando claramente a

   ■

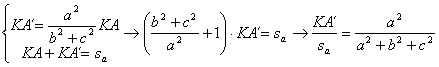Por otra parte, hacia el final de la resolución de este problema utilizaremos una de las conocidas desigualdades de J.C. Gerretsen

para cuya demostración se puede ver el artículo del extra 400 de esta revista publicado por el autor de estas líneas.

Centrándonos ahora en el problema sea  la altura relativa al vértice A sobre el lado BC, A´ el pie de la simediana  que parte de A, y la altura trazada desde el simediano al ya mencionado lado BC. Por relaciones de semejanza de triángulos claramente tenemos que

Por otra parte, utilizando la conocida relación entre la simediana y la mediana que parten del mismo vértice A de un triángulo

la expresión anterior para  , utilizando el lema 2 se reduce a

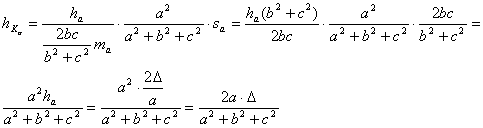
y expresiones análogas para  y . En consecuencia, tenemos que

donde hemos empleado la expresión  que se deduce inmediatamente a partir del lema 1 y de la identidad algebraica

Finalmente emplearemos una de las desigualdades de J. C. Gerretsen que establece ,  con lo que llegamos a

y esta última desigualdad es cierta ya que, claramente, a partir de la desigualdad de Gerretsen ya comentada, y la desigualdad de Euler , es claro que

lo que concluye la demostración.

---oooOooo---