Problema 536
3.- Construir las tres circunferencias que pasando por el punto de Gergonne son tangentes a dos de los lados del triángulo ABC.
Los seis puntos de tangencia son concíclicos.
Yiu, P. (2001): Introduction to the geometry of the triangle. (Versión 2.0402, abril 2002) , (p. 6)
Solución del director
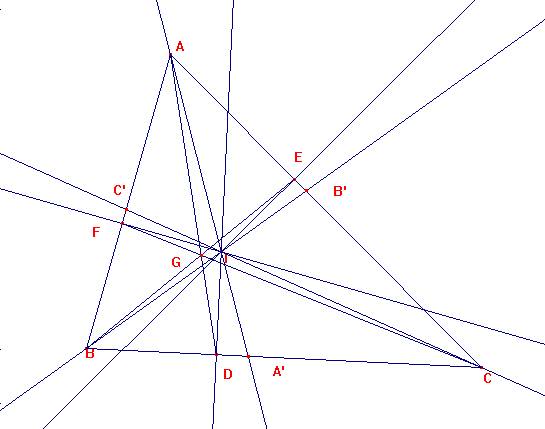
El punto de Gergonne es la intersección de las cevianas que van desde los vértices A,B,C a los puntos de tangencia D,E,F de la circunferencia inscrita con los lados.

La circunferencia que pasa por G y es tangente a BA y BC tiene el centro sobre la bisectriz BB’ y en la paralela a IE por G, por ser homotética con la inscrita.
Sea U dicho centro.
Tracemos por U una perpendicular a BA que cortará a AA’ en V.
Por V tracemos una paralela a IE (perpendicular a AC) que cortará a la bisectriz CC’ en W.
GUVW es paralelogramo por construcción, y GW es perpendicular a AB, por lo que W es el centro de la circunferencia que pasa por G y es tangente a CA y CB.
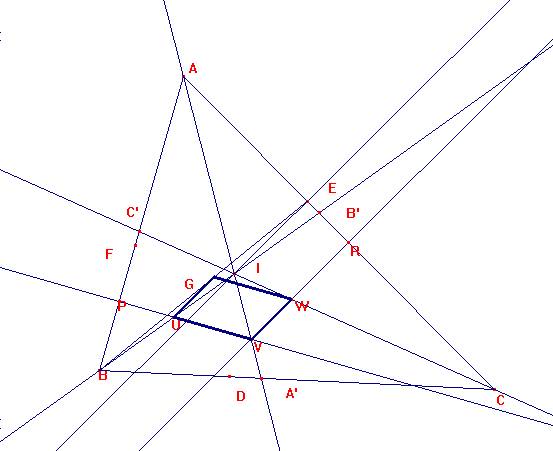
P, corte de UV con AB y R, corte de VW con AC, son dos de los puntos pedidos, que equidistan de la bisectriz AA’. AP=AR por tanto.
Si la tercera circunferencia es tangente a AB y AC en M y N, se tiene AM=AN.
Por ello, (AM)(AP)=(AN)(AR), y los puntos M,N,R,P son concíclicos.
Por analogía, si S y T son los puntos de contacto sobre BC, (CS)(CT)=(CR)(CN), y los puntos S, T,R y N son también concíclicos.
Además, cada bisectriz es mediatriz del par de puntos cercanos a cada vértice, de lo que se deduce que el incentro es centro de la circunferencia estudiada.
Ricardo Barroso Campos
Didáctica de las Matemáticas
Universidad de Sevilla