Problema 537
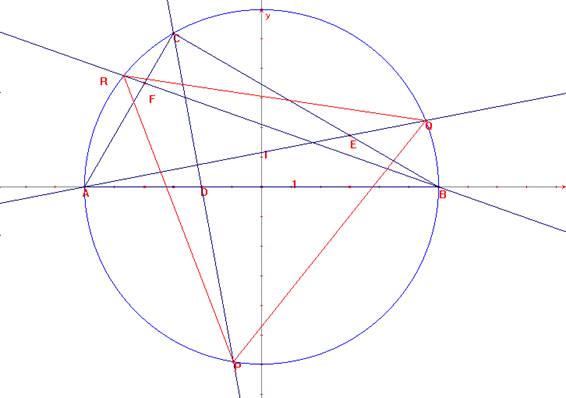
En un triángulo rectángulo ABC con <A=60º y B=30º, sean D,E,F los puntos de trisección cercanos a A, B y C sobre los lados AB, BC y CA, respectivamente. Extendemos CD, AE y BF hasta intersecar a la circunferencia circunscrita en P, Q y R. Demostrar que PQR es un triángulo equilátero.
Garfunkel, J. Pi,Mu Epsilon Journal 331 (26)
Solución del director
Tomemos el centro de la hipotenusa como centro de coordenadas.

Tomemos A(-6,0), B(6,0), C(-3, 3![]() ).
).
La circunferencia circunscrita es ![]()
Es D(-2,0), y la ecuación de CD es![]()
Los puntos de intersección de la recta CD y la circunferencia circunscrita son
C(-3, 3![]() ) y
) y 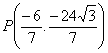
Por otra parte, es ![]() , y la ecuación de AE es
, y la ecuación de AE es ![]() .
.
Los puntos de intersección de la recta AE y la circunferencia circunscrita son
A(-6,0) y ![]() .
.
Por último, es ![]() , y la ecuación de BF es
, y la ecuación de BF es ![]() .
.
Los puntos de intersección de la recta BF y la circunferencia circunscrita son
B(6,0)
y ![]() .
.
Por último, es ![]() , cqd.
, cqd.
Ricardo Barroso Campos
Didáctica de las Matemáticas.
Universidad de Sevilla.