Problema 538.-
Homenaje a Jack Garfunkel
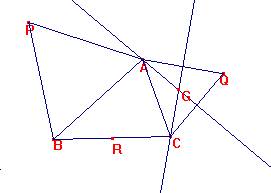
Dado un triángulo ABC se trazan equiláteros exteriores BAP y ACQ sobre los lados AB y CA. Sea R el punto medio de BC y G el baricentro de ACQ. Demostrar que el triángulo PRG es 30º-90º-60º.
Garfunkel, J. Pi Mu Epsilon, 44, 553
Solución del director.

Tracemos las paralelas la simétrica central de la figura según el centro R.
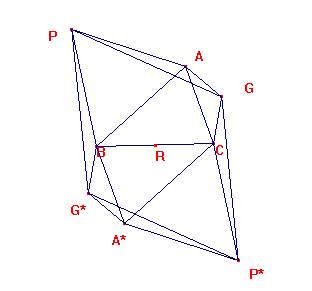
El triángulo AGP se transforma por un giro de centro G y ángulo de 120º en CGP*.
El triángulo GCP* se transforma por un giro de centro P* y ángulo de 60º en G*A*P*.
Por último, el triángulo G*A*P* se transforma por un giro de centro G* y ángulo120º en C*BP.
Así la figura PGP*G* es un rombo de ángulos 120º y 60º.
Su centro es R, y c.q.d., PRG es 30º-90º-60º.
Ricardo Barroso Campos
Didáctica de las Matemáticas
Universidad de Sevilla.