Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas del IES "Abastos" (Valencia)
Problema 540
Resolver y construir el triángulo rectángulo ABC, A=90º conocidos c, a+b.
Sánchez-Rubio, C. , Ripollés, M. (2000). Manual de matemáticas para preparación olímpica.Universitat Jaume I. Castelló. Problema 8 (pág. 339)
Ampliación del profesor Peiró:
Resolver y construir el triángulo rectángulo ABC, A=90º conocidos c, a-b.
Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de
Dibujo del IES
a)
Resolver y construir el triángulo rectángulo ABC, A=90º conocidos c,
a+b.
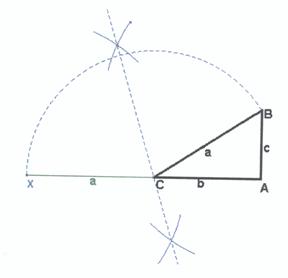 Partiendo
del problema resuelto, Se gira el vértice B -siendo el vértice C el centro de
giro- hasta que quede alineado con el lado b de modo que el resultado sea el
punto X y se cumpla: XA = a + b. La
mediatriz del segmento XB pasa por el punto C porque el segmento XB es la
cuerda del arco de giro del vértice B y la mediatriz de una cuerda pasa por el
centro de la circunferencia: el centro de giro C.
Partiendo
del problema resuelto, Se gira el vértice B -siendo el vértice C el centro de
giro- hasta que quede alineado con el lado b de modo que el resultado sea el
punto X y se cumpla: XA = a + b. La
mediatriz del segmento XB pasa por el punto C porque el segmento XB es la
cuerda del arco de giro del vértice B y la mediatriz de una cuerda pasa por el
centro de la circunferencia: el centro de giro C.
El definitiva se sitúa el XA = a+b y el segmento c ambos concurrentes en el vértice A = 90º. La mediatriz entre X y B cortará al segmento AX en el punto C. Tendrá solución si a+b > c
b)
Resolver y construir el triángulo rectángulo ABC, A=90º conocidos c,
a-b.
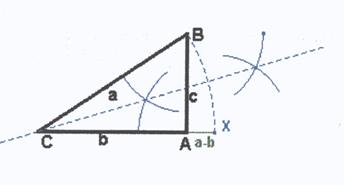 Volviendo
a partir del problema resuelto, Se gira el vértice B del mismo modo pero con
sentido contrario al ejercicio anterior de modo que se cumpla: XA = a - b. También la mediatriz del segmento XB
pasa por el punto C por el mismo motivo que el caso anterior.
Volviendo
a partir del problema resuelto, Se gira el vértice B del mismo modo pero con
sentido contrario al ejercicio anterior de modo que se cumpla: XA = a - b. También la mediatriz del segmento XB
pasa por el punto C por el mismo motivo que el caso anterior.
El definitiva se sitúa el XA = a - b y el segmento c ambos concurrentes en el vértice A = 90º. La mediatriz entre X y B cortará a la recta AX en el punto C. Tendrá solución si a - b < c