Propuesto por Gennaro Rispoli, profesor de matemáticas en el Liceo Scientifico Sperimentale annesso al Liceo Ginnasio "T.L. Caro", 84087 Sarno (Salerno), Italia.
Problema 542
Problema IR7
8.- Sea P un punto sobre la circunferencia circunscrita del triángulo
ABC. Es conocido que los pies de las perpendiculares trazadas por P a los lados
AB, BC y CA están alineados en la recta de Simson. Demostrar que las rectas de
Simson de dos puntos P1 y P2 diametralmente opuestos son perpendiculares.
“Baltic Way –
Solución del director.
Sin pérdida de generalidad, sea P1 sobre el arco AC que no
contiene a B, por ejemplo.
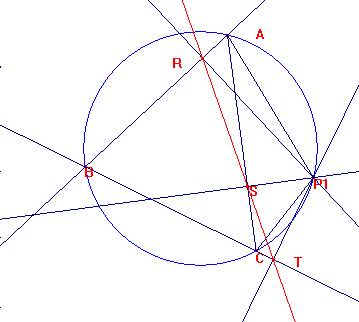
Sean R el pie de la perpendicular por P1 a AB y S el pie de
la perpendicular por P1 a AC.
El cuadrilátero ARSP1 es cíclico.
Por ello, ÐASR= ÐAP1R=90-ÐBAC-ÐCAP1.
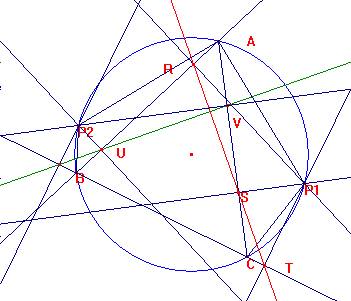
Sea P2 el diametralmente opuesto a P1.
Sea U el pie de la perpendicular por P2 a AB y V el pie de
la perpendicular por P2 a AC.
El cuadrilátero P2AVU es cíclico.
Por ello, ÐCVU=180-ÐAVU=ÐAP2U =90-ÐBAP2
=ÐBAP1
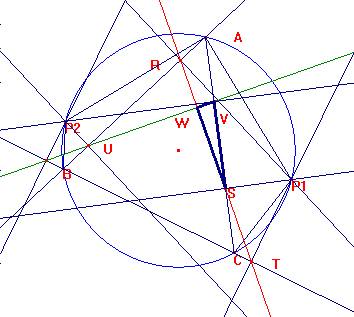
Así si W es el punto de corte de las rectas de Simson
correspondientes, es:
ÐVSW=ÐASR =90-ÐBAP1
ÐSVW=ÐCVU=ÐBAP1
Y por ello, ÐVWS=90, cqd.
Ricardo Barroso Campos
Didáctica de las Matemáticas
Universidad de Sevilla