Problema 545

265.- Encontrar en el interior de un triángulo dado un punto tal que los segmentos que lo unen a los vértices del triángulo dividen al inicial en tres triángulos cuyas áreas sean iguales.

Problema 545

265.- Encontrar en el interior de un triángulo dado un punto tal que los segmentos que lo unen a los vértices del triángulo dividen al inicial en tres triángulos cuyas áreas sean iguales.

Alexandroff, I. (1899) Problemas de geometría elemental agrupados según los métodos a emplear para su resolución. Traducido del ruso al francés, según la sexta edición por D. Aitoff. París (p. 56)

Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES La Serna de Fuenlabrada

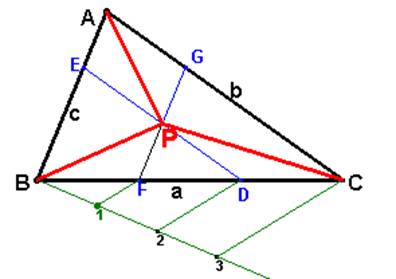Al hacer la paralela DE al lado b que esté a una distancia de 1/3 de la altura Hb, se habrá conseguido el lugar geométrico de los vértices, tal que, al unir un punto del segmento DE con los vértices C y A, se forma un triángulo de superficie 1/3 del dado.

Del mismo al hacer la paralela FG al lado c que esté a una distancia de 1/3 de la altura Hc, se habrá conseguido el lugar geométrico de los vértices, tal que, al unir un punto del segmento FG con los vértices A y B, se forma un triángulo de superficie 1/3 del dado.

Por lo tanto el punto P buscado estará en la intersección del los segmentos DE y FG.

Como el porcentaje de superficie que corresponde a cada lado por la partición es el mismo, el punto P coincide con el baricentro