Propuesto por Juan Bosco Romero Márquez, profesor
colaborador de la Universidad de Valladolid
Problema 546.- Sea ABC un
triángulo y AAa, la bisectriz interior del ángulo A, siendo Aa
su pie sobre el lado BC.Sean Ba y Ca, los puntos
obtenidos por intersección de la perpendicular que pasa por Aa y
corta al lado AC y AB, respectivamente. Definimos los puntos Da=AAa
y BaCa, Ea=AaBa y CCa,
Fa=AaCa y BBa. Probar que:
a) La altura desde A a BC
y las rectas BBa y CCa concurren en el punto Xa.
b) ¿Están
los puntos Ia=ABa · AaCa, Ja=AB
·DaFa, y Ka=BaCa · BC
alineados?
c) Haciendo
las mismas construcciones para los vértices B y C, y sus lados opuestos y con
las notaciones anteriores, obtenemos el triángulo XaXbXc.
¿Qué relación existe entre triángulo y el triángulo ABC?
Romero, J.B. (2010):
Comunicación personal.
Solución de
Saturnino Campo Ruiz, profesor del I.E.S Fray
Luis de León (Salamanca) de las dos primeras partes.
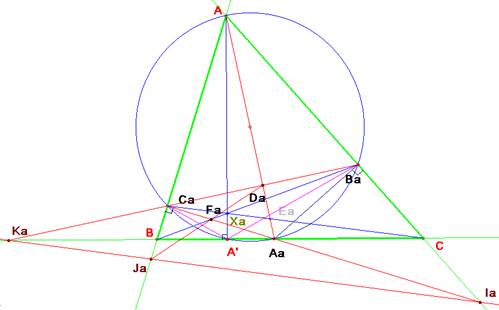
a) Tomamos la circunferencia circunscrita al
cuadrilátero ACaAaBa, que también contiene al pie A’ de la altura. Por ser el diámetro una bisectriz, los triángulos
rectángulos ACaAa y ABaAa son iguales y por tanto también son
iguales los ángulos ![]() AA’Ba y
AA’Ba y ![]() AA’Ca. Esto nos
recuerda que en el problema nº 71 de esta revista se demostró el
AA’Ca. Esto nos
recuerda que en el problema nº 71 de esta revista se demostró el
71.- Teorema de Blanchet.
En todo triángulo ABC de altura BH, al trazar las cevianas AM y CN
concurrentes con BH, se establece que la altura será bisectriz del ángulo MHN.
Un
recíproco de este teorema nos debe dar ahora que para la altura AA’, bisectriz del ángulo ![]() Ca A’Ba, las cevianas BBa
y CCa
concurren en un punto Xa.
Ca A’Ba, las cevianas BBa
y CCa
concurren en un punto Xa.
De no
ser así si llamo X’= BBa·AA’, proyectando el
punto C por éste, sobre AB se tendría otro punto C’a de modo
que, según el teorema de Blanchet, AA’sería
bisectriz de ![]() C’aA’Ba con lo cual C’a = Ca y en
consecuencia X’= Xa y queda
probada esta primera parte.
C’aA’Ba con lo cual C’a = Ca y en
consecuencia X’= Xa y queda
probada esta primera parte.
b) Si se proyectan los vértices B y C sobre el lado
opuesto, a través de la altura, definimos una proyectividad entre las rectas AB y AC,
en la que el punto común A, es fijo,
y por tanto, se trata de una perspectividad. El centro de esta perspectividad
es el punto donde concurren las rectas que unen cada punto con su homólogo. Son
pares de homólogos (Ca,Ba) y (B,C) y por tanto, el centro de esta perspectividad es el punto Ka y la cuaterna (KaA’BC) es armónica.
El método seguido en el problema
para definir los puntos Ia y Ja también define una proyectividad entre los lados del
triángulo concurrentes en A.
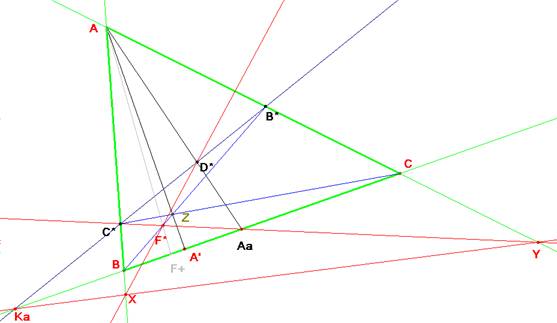
Dado un punto Z sobre la altura AA’. Defino los puntos siguientes: B*=BZ·AC, C*=CZ·AB,
D*=B*C*·AAa, F*=BB*·AaC* y a partir de ellos X=F*D*·AB e Y=AC·AaC*. La
homografía definida es X à Y.
Si se toma Z=A, B*=C*=D*=F*=A, y también X=Y=A, que nos indica que la aplicación
definida es una perspectividad.
Si se toma ahora Z=A’, B*=C y C*=B, el punto D*=B*C*·AAa= Aa, F*= F+ (un
punto de AaB), el punto X=F*D*·AB=B y el punto Y=AC·AaB=C.
Las dos transformaciones tienen dos pares de
homólogos iguales, si comparten un tercero es que son dos definiciones
diferentes de la misma homografía, una perspectividad de centro Ka , y con esto tendríamos
concluida la alineación pedida.
Para ello tomamos ahora Z=H el ortocentro del triángulo. Con el uso de las coordenadas baricéntricas
vamos a demostrar que los puntos generados Ia’ y Ja’ están alineados con Ka y con ello concluiríamos esta segunda parte.
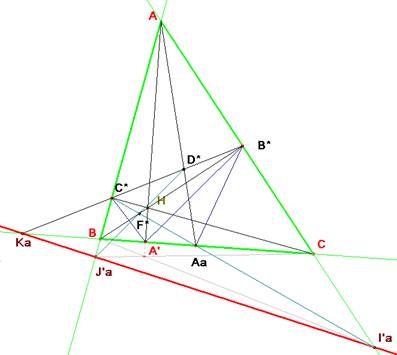
Las coordenadas baricéntricas
homogéneas respecto al triángulo ABC, de los distintos objetos geométricos
que intervienen son:
Puntos:
Pie de la bisectriz Aa=(0:b:c); Ortocentro
H=![]() ;
;
Pie de la altura desde C, C*=![]() ; Idem desde B, B*=
; Idem desde B, B*=![]() ;
;
Rectas:
C*Aa ![]() ; B*Aa
; B*Aa
![]() ; Bisectriz AAa
; Bisectriz AAa ![]() ; B*C*
; B*C*![]() BB*
BB* ![]() ; CC*
; CC*![]() AC
AC![]() AB
AB![]()
Por último:
D*= AAa· B*C* =![]() ; F*=
BB*·AaC*=
; F*=
BB*·AaC*=![]() , D*F*
, D*F* ![]()
En todo lo anterior se toma ![]() y expresiones análogas para
y expresiones análogas para ![]() y
y ![]() .
.
I’a es la
intersección con AC de AaC* se obtiene: I’a=![]()
Ja’ es la intersección de F*D* con
BA: Ja’=![]()
Ka es la
intersección de B*C* con BC: Ka= ![]()
La alineación de estos puntos significa la anulación
del determinante formado por sus coordenadas:
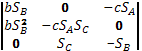 =
=![]() .
.
Puede comprobarse también que
las rectas ![]() y
y ![]() concurren con la altura AA’.
concurren con la altura AA’.
Y con esto concluimos.![]()