Problema  547

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triángulo. Sea  la probabilidad pedida. Usaremos las conocidas fórmulas de Apolonio para las longitudes de las medianas de un triángulo en función de sus lados, que se obtienen fácilmente a partir del teorema de los cosenos

                         

y las bien conocidas relaciones , , , de donde es inmediato comprobar que se cumple

Emplearemos también un resultado fundamental que ya apareció como problema 140 de esta misma revista (y que por tanto no volveremos a demostrar) que plantea el siguiente teorema.

Teorema: “Sea P un punto del plano de un triángulo ABC y sea G su baricentro. Entonces se tiene la identidad ”.

A partir del teorema anterior, es claro que para todos los puntos de una circunferencia con centro en el baricentro, la suma de los cuadrados de sus distancias a los vértices es constante. Obviamente, esta suma de cuadrados va en aumento a medida que el radio de la circunferencia centrada en dicho punto es cada vez mayor. Consideremos la circunferencia con centro en el baricentro G y de radio tal que pasa por el vértice B. Por las propiedades elementales relativas a las medianas, sabemos que este radio corresponde a . Sean E y D los pies de las perpendiculares desde el baricentro G a los lados AC y BC, respectivamente. Sean S y Q los puntos de corte de dicha circunferencia (más cercanos al vértice C) con los lados AC y BC, respectivamente. Es claro entonces que la probabilidad pedida será igual al cociente entre el área del “triángulo curvilíneo” SCQ entre el área del triángulo original ABC ya que para todos los puntos P de la circunferencia centrada en el baricentro y de radio  se tiene entonces que

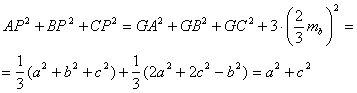
La probabilidad pedida vendrá dada  claramente entonces por la siguiente expresión, donde todos los corchetes representan áreas de triángulos y  representa el área del sector circular GSQ.

Por otra parte, es inmediato obtener, aplicando el teorema de Pitágoras, y teniendo en cuenta que  y  las longitudes de los segmentos AE, ES, BD, DQ de manera que tenemos

                   

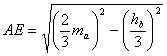
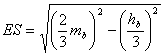
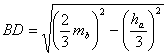
                [1]

Sean  y . Considerando el cuadrilátero DGEC y observando que los ángulos en E y en D son rectos, se tiene

Finalmente, teniendo en cuenta que por las propiedades elementales de las medianas el área del triángulo AGB es la tercera parte del área del triángulo ABC, y agrupando los triángulos AGE y GES como uno único y lo mismo con los triángulos BGD y DGQ, llegamos a la expresión de la probabilidad pedida

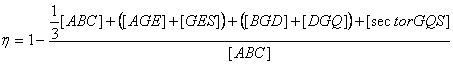
donde se cumple que

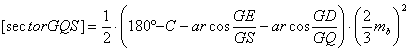
Claramente hemos llegado a una expresión para la probabilidad pedida que se puede escribir fácilmente en función de los elementos del triángulo original ABC al aplicar [1], por ejemplo, en función exclusiva de los lados del triángulo, etc.

---oooOooo---