Problema 548.- (Propuesto por Gennaro Rispoli, Salerno, Italia)

            El triángulo ABC tiene ortocentro H. Los pies de las perpendiculares desde H a las bisectrices interna y externa del ángulo BAC (que no es recto) son P y Q. Demostrar que PQ pasa por el punto medio de BC.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo de la resolución del problema, utilizaremos la notación habitual en la geometría del triángulo. Sean H el ortocentro del triángulo ABC. Sea P la proyección de H sobre la bisectriz exterior, sea Q la proyección de H sobre la bisectriz interior, y sea R el punto medio del lado BC. Sea también D el punto de intersección de la bisectriz interior (distinto de A) con la circunferencia circunscrita al triángulo, que como es bien conocido, corresponde al punto medio del arco BC.

Consideremos el triángulo AOD, que, obviamente, es isósceles, por tener dos lados iguales al radio de la circunferencia circunscrita al triángulo ABC. Utilizando propiedades elementales relacionadas con los ángulos inscritos en una circunferencia, es fácil obtener que , y en consecuencia también

            Por otra parte, es inmediato observar que , por ser alternos internos, y entonces también , ya que PAQH es claramente un rectángulo. En consecuencia, la proposición quedará demostrada si somos capaces de probar que en la construcción inicial, se cumple . Para ello, es fácil, teniendo en cuenta que ,  y relaciones trigonométricas elementales, obtener las siguientes expresiones

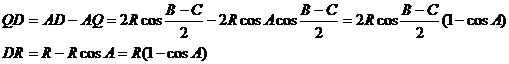
            Finalmente, aplicando el teorema de los senos al triángulo QDR, y denotando ,  podemos plantear las relaciones

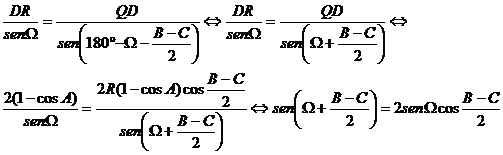
que es cierta (utilizando las fórmulas del ángulo doble) para . Además, el ángulo , es claramente agudo, y una simple reducción al absurdo demuestra que es la única solución válida para nuestro problema, ya que si suponemos otro ángulo , distinto de  y cumpliendo la misma relación, tenemos que

                     

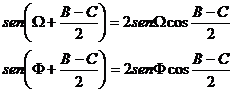
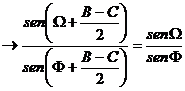
lo que nos lleva, después de simplificar los senos de sumas de ángulos a

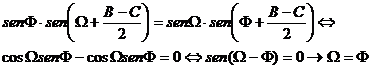
en contradicción, con lo supuesto. Esto demuestra que  y concluye la demostración.

---oooOooo---