Problema 549

Ejercicio 7 Un problema de construcción : triángulos homotéticos

Sea ABC un triángulo dado

Sea MNP un triángulo inscrito en ABC, con M en BC, N en CA y P en AB.

Construir un tercer triángulo A'B'C' inscrito en MNP tal que los lados homólogos sean paralelos, es decir, A' en NP, B' en PM, C' en MN, A'B' paralelo a AB, B'C' paralelo a BC, y C'A' paralelo a CA.

Sortais, Y et R (1993): Géométrie de l'espace et du plan : synthese de cours, exercices résolus (p. 103)

Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES La Serna de Fuenlabrada

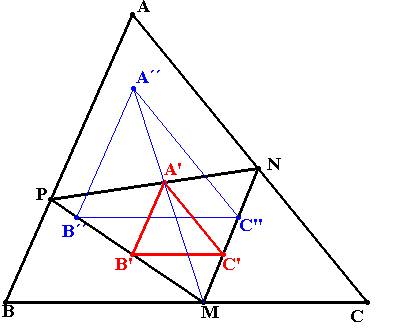Al considerar el punto M como centro de homotecia, y un triángulo cualquiera A”B”C” homotético de la solución, los vértices B” y C” cumplirán:

1. B” y C” estarán respectivamente en las rectas MP y MN puesto que dos puntos homotéticos están alineados con el centro de homotecia M
2. B”C” formarán un segmento paralelo a BC.

Para la construcción se traza una recta paralela a la base BC por un punto cualquiera B” de MP y donde corte a MN resultará en vértice C”, se completa el triangulo A”B”C” por paralelismo. Al hallar el vértice homotético de A” que pertenezca a PM resultará el vértice solución A´ y por paralelismo salen B´y C´.