Problema 549

Ejercicio 7 Un problema de construcción : triángulos homotéticos

Sea un triángulo dado

Sea un triángulo inscrito en , con M en BC, N en CA y P en AB.

Construir un tercer triángulo inscrito en tal que los lados homólogos sean paralelos, es decir, A' en NP, B' en PM, C' en MN, A'B' paralelo a AB, B'C' paralelo a BC, y C'A' paralelo a CA.

Sortais, Y et R (1993): Géométrie de l'espace et du plan : synthese de cours, exercices résolus (p. 103)

Solución Ricard Peiró:

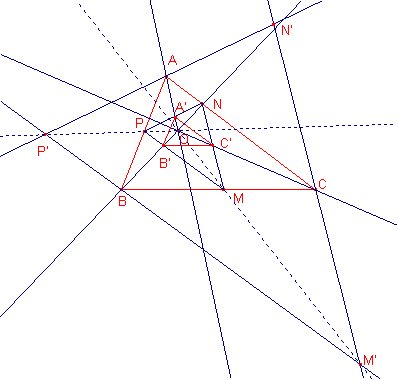
Construimos el triángulo tal que sea paralelo a , paralelo a , paralelo a .

Los triángulos , son homotéticos.

El centro O de homotecia es la intersección de las rectas PP’, MM’.

El triángulo está inscrito en el triángulo . El triángulo (inscrito en el triángulo) es homotético al triángulo y tiene el mismo centro de homotecia.

La recta OA intersecta el lado en el punto A’.

La recta OB intersecta el lado en el punto B’.

La recta OC intersecta el lado en el punto C’.