Problema 551

Las distancias de un punto cualquiera de una mediana a los lados que parten del mismo vértice son inversamente proporcionales a dichos lados.

Frère Gabriel Marie , 1820-1891. 5. ed.:  3 p. L., [iii]-xxiv, 1302 p. diagrs. 22 cm .
Tours, A. Mame et fils; [etc., etc.] 1912. (p.757)

Solución de Ricard Peiró i Estruch.

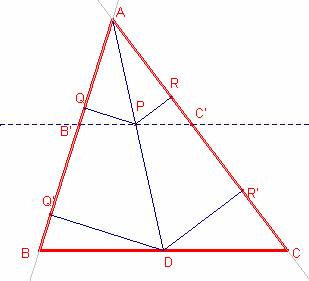
Sea el triángulo . Sea la mitjana .

Sea P un punto cualquiera de la mediana .

Siqa Q la proyección de P sobre . Sea R la proyección de P sobre .

Queremos probar que .

Sea Q’ la proyección de DP sobre . Sea R’ la proyección de D sobre .

Sea la recta paralela al lado que pasa pel punto P.

La recta corta los lados , en los puntos B’, C’, respectivamente.

Els triángulos , son homotéticos.

Entonces, . Entonces, (1)

Los triángulos , tienen la misma área.

Entonces, . Entonces, (2)

De las expresiones (1) (2): . Entonces, .

Con Cabri:

Figura barroso551.fig

Applet created on 1/03/10 by Ricard Peiró with CabriJava