Problema 551.- Las distancias de un punto P cualquiera de una mediana a los lados que parten del mismo vértice son inversamente proporcionales a dichos lados.

Frére Gabriel Marie; 1820-1891; 5ª ed.: 1302p. Tous, A. Maure et fils. 1912. (p. 757).

Resolución : Vicente Vicario García, I.E.S. El Sur, Huelva

A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triángulo. Sea P un punto interior cualquiera de la mediana que parte del vértice A. Sea A´ el pie de la mediana sobre el lado BC. Sean D y E las proyecciones ortogonales de este punto sobre los lados AB y AC (o sobre sus prolongaciones), respectivamente. Sea , con . Sean y los ángulos que forma la mediana con los lados AC y AB, del triángulo, respectivamente. Es inmediato observar que, y .

Aplicando ahora el teorema de los senos a los triángulos AA´C y BAA´, tenemos

[1]

[2]

De esta forma, utilizando las relaciones anteriores [1] y [2], y denotando por el área de triángulo ABC, tenemos fácilmente que

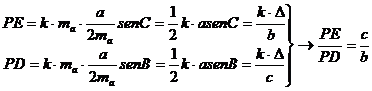
que es lo que se quería demostrar.

Si el punto P elegido sobre la mediana es exterior al triángulo, la relación anterior sigue siendo válida ya que ésta se mantiene ante una homotecia.

---oooOooo---