(Propuesto por Vicente Vicario García, I.E.S. El Sur, Huelva)

Problema 553

Vicario, V(2010): Comunicación personal

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

            A lo largo del problema utilizaremos la notación habitual en la geometría del triángulo. Sea ABC un triángulo escaleno arbitrario con . Son bien conocidas las expresiones clásicas para las longitudes de las medianas del mismo en función de sus lados (que se pueden deducir sin más aplicar el teorema de los cosenos) y que vienen dadas por (teorema de Ptolomeo)

               

con lo que es claro que puesto que , entonces . Por tanto, la mediana (que divide al triángulo en dos partes de igual área) de menor longitud es .

            Sea ahora PQ un segmento con P en AB y Q en AC de manera que divida al triángulo en dos partes de igual área. Sea  y . Puesto que el segmento PQ divide en dos partes de igual área el triángulo, tenemos que

            Aplicando el teorema de los cosenos al triángulo PAQ, tenemos que

con lo que podemos expresar PQ en función exclusivamente de t, obteniéndose

            Intentaremos minimizar la expresión PQ para valores . Para ello, definimos la función  en  y determinamos su derivada , que se anula para . En este punto, tenemos un mínimo relativo, ya que .

 Por otra parte, los valores de la función en los extremos del intervalo  son

,  

 y

.

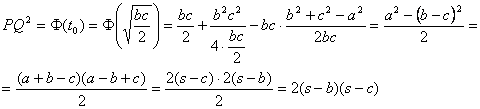Además, es fácil ver que PQ es menor que el valor en los extremos, con lo que tenemos un mínimo absoluto en .

De forma análoga, si suponemos los segmentos MN ( M en AB y N en BC) y RS (R en BC y S en AC) que dividen al triángulo en dos partes de igual área, obtenemos

           

y claramente tenemos que , y .

            Por último, veamos que el segmento es siempre menor que la mediana de menor longitud, es decir , ya que

con lo que el segmento lineal de menor longitud que divide al triángulo ABC en dos partes de igual área es el segmento , con R en el lado BC y S en el lado AC.

---oooOooo---