Propuesto por William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú.

Problema 554

En un triángulo ABC se tiene: <BAC=80º, <BCA=20º, y sea D el pie de la bisectriz del ángulo B.

Demostrar que DC=AB+BD.

Rodríguez, W. (2010): Comunicación personal.

Solución de Milton Donaire Peña

Lima Perú 01 04 2010

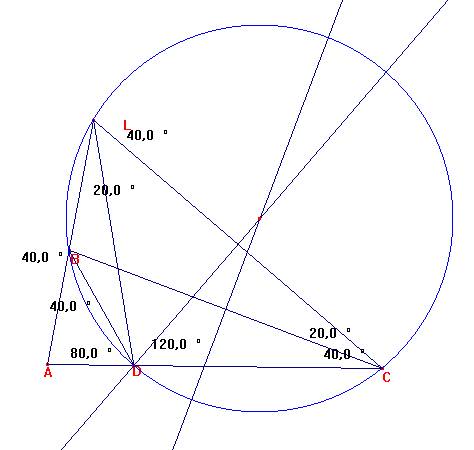
Tracemos por D el segmento DL de manera que <ADL=80º.

Así DBL es isósceles y AL=AB+BL=AB+BD.

El triángulo ADL es isósceles.

Es: <LBC=100º=<LDC, por lo que el cuadrilátero LBDC es inscriptible.

Así, <DLC=<DBC=40º. Luego LDC es isósceles.

De todo ello, se deduce que DC=DL=LA=AB+BD.