Problema 554.- (Propuesto por William Rodríguez Chamache, profesor de geometría de la “Academia integral  class”, Trujillo, Perú.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

            Utilizaremos la notación habitual en la geometría del triangulo. Es claro que  ya que  y , y en consecuencia, el triángulo dado ABC es isósceles. Sin perdida de generalidad, sea . Aplicando el teorema de los senos al triangulo ADB tenemos que

                 [1]

            Aplicando de nuevo el mismo teorema al mismo triángulo, y teniendo en cuenta que BD es la bisectriz interior que parte del vértice B, tenemos

                 [2]

            Teniendo en cuenta el triángulo isósceles ABC, y como, es claro que

                                                       [3]

y en consecuencia, como , demostrar que , es equivalente a demostrar, teniendo en cuenta [1], [2] y [3], que

           

y la ultima relación trigonométrica es cierta ya que, a partir de la expresión para el seno del ángulo triple, relaciones trigonometricas del ángulo doble y trigonometría elemental, sustituyendo , tenemos precisamente esta identidad.

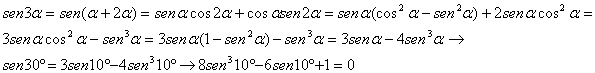
---oooOooo---