Problema 555.
Siga ![]() un triangle rectangle
un triangle rectangle ![]() . Siga P sobre
. Siga P sobre ![]() .
.
Siguen I, J els peus de les perpendiculars traçades per P a ![]() ,
, ![]() , respectivament.
, respectivament.
Com hem d’escollir P a fi que ![]() siga mínim?.
siga mínim?.
Solució1 Ricard Peiró.
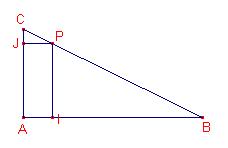
Notem que AIPJ és un rectangle.
![]()
Aleshores la mínima distància s’assoleix quan la distància de A a la recta BC és mínima.
És a dir quan ![]() és l’altura del triangle rectangle sobre la hipotenusa.
és l’altura del triangle rectangle sobre la hipotenusa.
![]() .
.
Solució 2:
Siga ![]() ,
, ![]() .
.
![]() .
.
Els triangles ![]() ,
, ![]() són semblants. Aplicant el teorema de Tales:
són semblants. Aplicant el teorema de Tales:
![]() .
.
Aleshores, ![]()
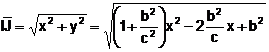 .
.
El valor mínim de ![]() s’assoleix en el vèrtex de la paràbola còncava
s’assoleix en el vèrtex de la paràbola còncava
![]() .
.
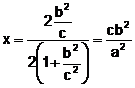 . En aquest cas
. En aquest cas ![]() .
.
La mesura del segment ![]() és
és ![]() .
.
Notem que ![]() , és a dir,
, és a dir, ![]() i
i ![]() són perpendiculars.
són perpendiculars.