Problema 555
3.1 El triángulo rectángulo
Sea ABC un triángulo rectángulo con el ángulo recto en el vértice A, y P sobre BC. Sean I y J los pies de las perpendiculares trazadas por P a AB y AC. ¿Cómo debemos elegir P para que IJ sea mínimo?
Laborde, C. (1992): Solving problems in computer based geometry enviroments: The influence of the features of the software. ZDM (92/4), p. 131
Solución 1 Ricard Peiró.
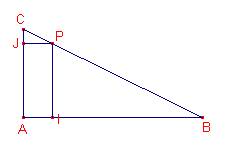
Notemos que AIPJ és un rectángulo.
![]()
Entonces la mínima distancia se alcanza cuando la distancia de A a la recta BC es mínima.
Es decir cuando ![]() és l’altura del triángulo rectángulo sobre la hipotenusa.
és l’altura del triángulo rectángulo sobre la hipotenusa.
![]() .
.
Solución 2:
Sea ![]() ,
, ![]() .
.
![]() .
.
Los triángulos ![]() ,
, ![]() son semejantes. Aplicando el teorema de Tales:
son semejantes. Aplicando el teorema de Tales:
![]() .
.
Entonces, ![]()
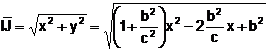 .
.
El valor mínimo de ![]() se alcanza en el vértice de la parábola cóncava
se alcanza en el vértice de la parábola cóncava ![]() .
.
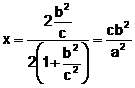 . En este caso
. En este caso ![]() .
.
La medida del segmento ![]() es
es ![]() .
.
Notemos que ![]() , es decir,
, es decir, ![]() y
y ![]() son perpendiculares.
son perpendiculares.