Problema 556

Propuesto por William Rodríguez Chamache. profesor de geometría de la "Academia integral class" Trujillo- Perú.

En un triángulo ABC se tiene que <BAC=60º-2β, <BCA=3β. Se tiene D en el segmento AC tal que

AB=DC y que <DBC=5β. Hallar β.

Rodríguez, W. (2010): Comunicación personal.

Solución del director.

Es <BCA=3β, <CBD=5β, <CAB=60-2β, <DBA=120º-6β

Tracemos la simétrica de toda la figura respecto a la mediatriz de AC.

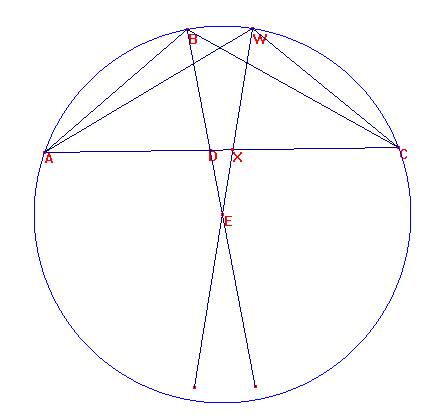
Es: AX=CW=CD=AB.

<WBC=<WAC=3β. <CBD=5β, por lo que <DBW=8β.

De igual manera, <XWB=<XWA+<AWB=5β+<ACB=5β+3β, por lo que el triángulo EBW es isósceles y <BWE=180º-16β.

Por tanto, podemos hacer la hipótesis inicial de que E sea el circuncentro de ABC.

Tracemos EA. El ángulo <BEA debería ser igual a 2<BCA=2*3β=6β,

Y sería: <EAD= 180º-(<BEA)-(<EBA)-(<BAD)=180º-(6β)-(120º-6β)-(60º-2β)=2β.

Por otra parte, EBC también debería ser isósceles según la hipótesis establecida.

Luego <ECB=<EBC=5β. Luego sería <ECD=<ECB-<DCB=5β-3β=2β.

Así EAB sería equilátero.

Por lo tanto el triángulo EAC es isósceles y E confirma la hipótesis establecida.

Veamos que se verifica completamente el enunciado.

<EDC es ángulo exterior en el triángulo BDC, por lo que su valor es la suma de los no adyacentes: <EDC=<DCB+<BCD=8β. Luego ECD es isósceles.

Por ello, es DC=EC=EA= AB, cqd

Así al ser EAB equilátero es 6β=60º, y por último, β=10º

Ricardo Barroso Campos

Didáctica de las Matemáticas.

Universidad de Sevilla