Problema 556.- (Propuesto por William Rodríguez Chamache, profesor de geometría de la Academia Integral Class “Trujillo”, Perú).

En un triangulo ABC se tiene que , . Se tiene D en el segmento AC tal que y que . Hallar .

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triangulo. Sin perdida de generalidad, supondremos . Es claro entonces que

,

y también

y en consecuencia, tenemos que

Aplicando el teorema de los senos al triangulo ABD tenemos

[1]

y aplicando el mismo teorema al triangulo BDC tenemos entonces que

[2]

Igualando los valores de BD obtenidos de [1] y [2], y empleando identidades trigonometricas muy conocidas llegamos a la siguiente cadena de igualdades

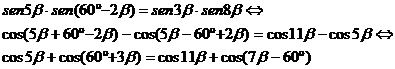
y es claro que la ultima igualdad es cierta para , ya que claramente tenemos que

lo que concluye el problema.

Nota: La ecuación trigonometrica admite una única raíz real positiva compatible con las condiciones del problema. Esto puede advertirse a partir de la representación grafica de la función .

---oooOooo---