Problema 557

Propuesto por Nicolás Rosillo Dpto. Matemáticas, IES Máximo Laguna (Santa Cruz de Mudela, Ciudad Real) y Francisco Javier García Capitán, profesor del IES Álvarez Cubero (Priego de Córdoba)

Para cualquier triangulo existen dos puntos tales que sus simétricos respecto los lados del triángulo forman un triángulo equilátero.

Rosillo, N, y García Capitán, F.J. (2010): Comunicación personal

Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES La Serna de Fuenlabrada

Análisis del problema resuelto

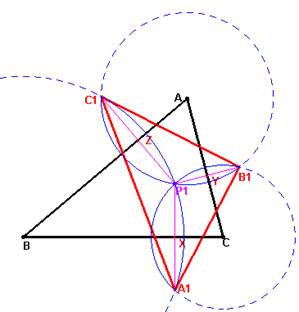
Tomemos el triángulo ABC y un punto cualquiera P1 interior al triángulo. Al hacer los puntos simétricos del punto P1 respecto de los lados a, b y c da como resultado el triángulo A1, B1 y C1 (prescindamos de que la solución sea un triángulo equilátero).

Por ser inscriptible el cuadrilátero A-Z-P1-Y, el ángulo C1-P1-B1 = Z-P1-Y vale 180-A, o sea el punto P1 pertenece al arco capaz de 180-A del segmento C1-B1, el centro de este arco capaz coincide con el vértice A puesto que las mediatrices de las cuerdas C1-P1 y P1-B1 son los lados c y b del triángulo. Por la misma razón C1-P1-A1 están en una circunferencia de centro el vértice B y A1-P1-B1 están en otra circunferencia de centro C; B y C son los centros de los arcos capaces de 180-B y 180-C de los segmentos C1-A1 y A1-B1.

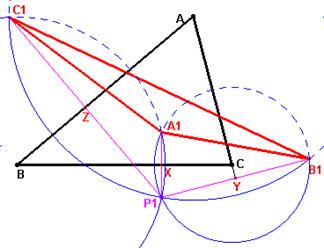
Sigamos con el problema resuelto, tomemos el punto P1 exterior al triángulo. Desde P1 el segmento C1-B1 se sigue viendo con un ángulo de 180-A pero los segmentos C1-A1 y A1-B1 se ven con un ángulo de B y C respectivamente. En esta posición, a pesar del cambio, los centros de los arcos capaces respecto al triángulo A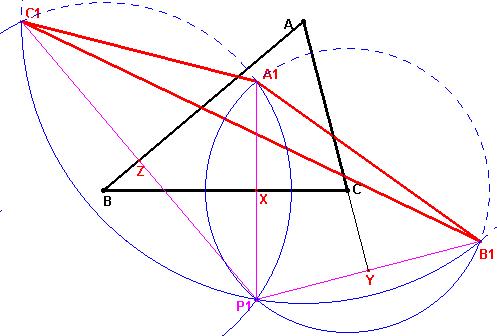1-B1-C1 son los mismos que en el caso anterior (la parte del arco capaz de 180-A, 180-B y 180-C de los lados a1, b1 y c1 está en el mismo semiplano que los vértices A1, B1 y C1).

Sin embargo si se alejara más el punto P1 del triángulo A1-B1-C1, se ordena en sentido contrario y los centros de los arcos capaces (referidos a los lados a1, b1 y c1) son los simétricos respecto de sus lados de los anteriores, (la parte del arco capaz de 180-A, 180-B y 180-C de los lados a1, b1 y c1 está en el semiplano contrario a los vértices A1, B1 y C1).

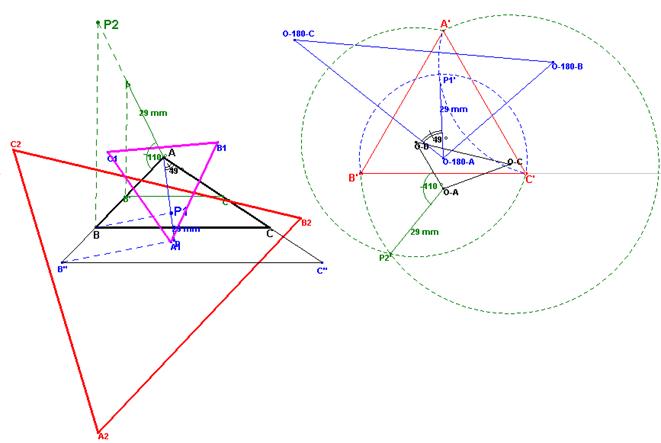
RESOLUCIÓN DEL PROBLEMA

Sea el triángulo ABC el dado y se pretende hallar el punto P1 y P2 para que los simétricos con respecto de los lados triángulos a, b y c den los triángulos equiláteros A1-B1-C1 y A2-C2-B2.

Se va a aplicar para la resolución el método del problema contrario. Como la forma de triángulo solución se conoce, se parte de un triángulo equilátero cualquiera A’-B’-C’ y se hallan los puntos P1’ y P2’ para que al hallar los simétricos respecto de los lados del triángulo auxiliar A’-B’-C’ y den triángulos semejantes al dado.

El triángulo formado por los centros de los arcos capaces de 180-A, 180-B y 180-C de los lados del triángulo equilátero forman un triángulo con una semejanza directa (ordenados los vértices en el mismo sentido) del dado, la intersección de los arcos capaces es el punto P1’. Al hallar los simétricos de los anteriores centros de los arcos capaces respecto de los lados se obtiene un triángulo con una semejanza inversa (ordenados los vértices en sentido contrario) del dado, la intersección de los arcos capaces es el punto P2’

Para ajustar los cálculos auxiliares al triángulo dado se ha utilizado dos homotecias cuyos centros son el vértice A.