Problema 557.- (Propuesto por Nicolás Rosillo, I.E.S. Máximo Laguna (Santa Cruz de Mudela, Ciudad Real) y Fco. Javier García Capitán, I.E.S. Álvarez Cubero (Priego de Córdoba)

Para cualquier triangulo existen dos puntos tales que sus simétricos respecto de los lados del triangulo forman un triangulo equilátero.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

A lo largo de la resolución del problema utilizaremos la notación habitual en la geometría del triangulo. Hay que decir que este problema es clásico en la literatura sobre la geometría del triangulo y se conoce su solución. Nosotros, lo resolveremos utilizando la geometría de coordenadas.

Sea ABC un triangulo dado y P un punto de su plano, de manera que sus distancias a los vértices A, B y C, sean x, y, z respectivamente. Sean también X, Y, Z las imágenes simétricas del punto P respecto de los lados AB, BC y AC del triangulo respectivamente. Es claro que el triangulo XAZ es isósceles y , por lo que . De forma análoga , .

Por tanto, si suponemos que XYZ es un triangulo equilátero, se debe cumplir que

,y en consecuencia, aplicando el teorema de los senos generalizado, se tiene que .

Por otra parte, el lugar geométrico de los puntos del plano cuyo cociente de distancias a dos puntos fijos es constante, es bien conocido y se reduce a una circunferencia cuyo centro pertenece al propio segmento o a su prolongación. Esto es fácil de demostrar, ya que, imponiendo esta condición tenemos que si nos fijamos, por ejemplo en el segmento AB, donde A y B son dos de los vértices del triangulo ABC, situando ejes coordenados de manera que el eje X pase por dicho segmento y el eje Y perpendicular al anterior y pasando por el punto medio de dicho segmento, las coordenadas de estos puntos son del tipo y , donde , y en consecuencia

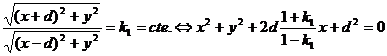
que es la ecuación de una circunferencia con centro 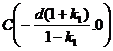y radio 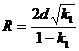. De esta forma, se pueden obtener los otros dos centros (que pertenecen a las líneas de los vértices del triangulo) y los radios de las dos circunferencias que faltan.

Es un trabajo analítico muy pesado demostrar que las tres circunferencias comentadas tienen sus centros alineados y se cortan en dos puntos exactamente, que son los puntos cuya existencia propone demostrar el problema.

---oooOooo---