In memoriam, al profesor Gennaro Rispoli

Problema 559

Sea P un punto del interior del triángulo ABC.

Sean D, E y F los pies de las perpendiculares desde P a BC, CA y AB, respectivamente.

Si los tres cuadriláteros AEPF, BFPD y CDPE tienen incírculos tangentes a los cuatro lados, demostrar que P es el incentro de ABC.

Rabinowitz, S. (2004):Crux Mathematicorum, Problem 2902. 30.1, (p.38)

Solución del director

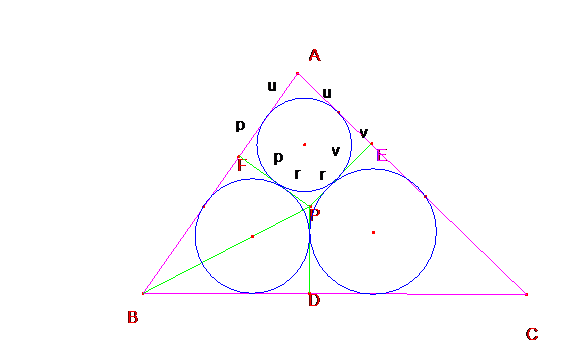
Consideremos el cuadrilátero AEPF.

Por ser AEP y AFP dos triángulos rectángulos con hipotenusa común, es:

(u+p)²+(p+r)² = (u+v)²+(v+r)².

Es decir, u² + 2up + p² + p² + 2pr + r² = u² + 2uv + v² + v² + 2vr + r²

O sea, 2up-2uv + 2p² - 2v² + 2pr -2vr=0. , up-uv + p² - v² + pr -vr=0.

(p-v) (u+p+v+r)=0.

Luego tenemos dos soluciones:

p=v, AF=AE, de donde AP es bisectriz de FAE, o

u+p+v+r=0, por lo que AF=0=AE, y el triángulo es el punto A.

De igual manera, CP y BP son bisectrices, y por ello, P=I, cqd

Ricardo Barroso Campos

Didáctica de las Matemáticas

Universidad de Sevilla