Problema 559

Siga P un punt interior al triángle .

Siguen D, E, F els peus de les perpendiculars des de P als costats , , , respectivament.

Si els quadrilàters AEPF, BFPD i CDPE tenen incercles tangents als quatre costats, demostreu que P és l’incentre del triangle .

Solució Ricard Peiró i Estruch.

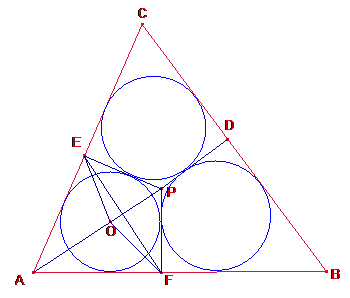
Siga O el centre de la circumferència tangent al quadrilàter AFPE.

O pertany a la bisectriu de l’angle A, a la bisectriu de l’angle recte i a la bisectriu de l’angle recte .

Vegem que P pertany a la bisectriu de l’angle A.

, .

Aleshores els triangles , , per tant, i .

Aleshores el triangle és isòsceles.

.

Aleshores, el triangle és isòsceles, per tant, .

Aleshores els triangles rectangles , són iguals.

Per tant, . Aleshores, P pertany a la bisectriu de l’angle A.

Anàlogament, P pertany a la bisectriu dels angles B i C. Aleshores, P és l’incentre del triangle .