Problema 559

Problema 559

Sea P un punto del interior del triángulo .

Sean D, E y F los pies de las perpendiculares desde P a , , , respectivamente.

Si los tres cuadriláteros AEPF, BFPD y CDPE tienen incírculos tangentes a los cuatro lados, demostrar que P es el incentro de .

Rabinowitz, S. (2004):Crux Mathematicorum, Problem 2902. 30.1, (p.38)

Solución Ricard Peiró i Estruch.

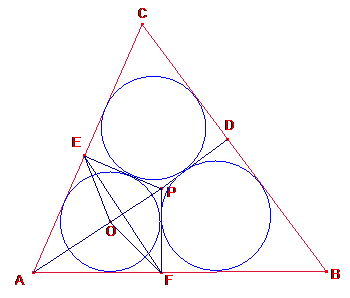
Sea O el centro de la circunferencia tangente al cuadrilátero AFPE.

O pertenece a la bisectriz del ángulo A, a la bisectriz del ángulo recto y a la bisectriz del ángulo recto .

Veamos que P pertenece a la bisectriz del ángulo A.

, .

Entonces los triángulos , , por tanto, i .

Entonces el triángulo es isósceles.

.

Entonces, el triángulo es isósceles, por tanto, .

Entonces los triángulos rectángulos , son iguales.

Por tanto, . Entonces, P pertenece a la bisectriz del ángulo A.

Análogamente, P pertenece a la bisectriz de los ángulos B y C. Entonces, P es el incentro del triángulo .