Problema 560
Trazar tres circunferencias que pasen por los vértices de un triángulo y los
puntos medios de los lados concurrentes. Unamos el centro de cada
circunferencia con el punto de corte de las otras dos circunferencias (el punto
medio del lado, pues en el punto de Miquel se cortan las tres) con un segmento.
Demostrar que los tres segmentos así obtenidos se intersecan en un único punto
que pertenece a la recta de Euler.
González Calvet, R.
(8/10/2000): TREATISE OF PLANE GEOMETRY THROUGH GEOMETRIC ALGEBRA (ed.
electrónica, 2000-2001, ed. impresa, 2007), problema 9.5.
El director añade que
Solución del director.
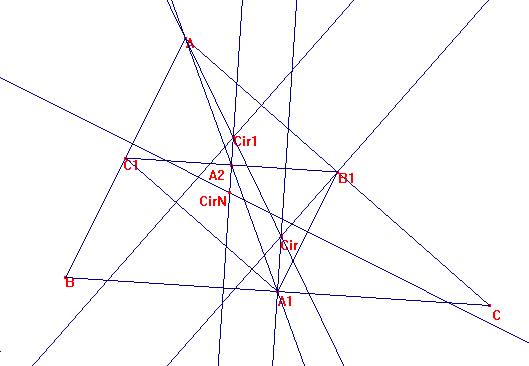
Sea ABC el triángulo inicial.
Sea A1B1C1 el medial.
Sea Cir el ciercuncentro de ABC y Cir1 el circuncentro de AB1C1
Sea A2 el punto medio de C1B1.
Los triángulos ACir1A2 y ACirA1 son semejantes con CirA1=2Cir1A2, y paralelos al ser perpendiculares a BC y C1B1.
El centro de la circunferencia de Euler o de Feuerbach o de los nueve puntos es CirN, que es el circuncentro de A1B1C1, por lo que es el simétrico de Cir1 respecto a C1B1.
Así tenemos que Cir1CirN =CirA1, y ambos segmentos son paralelos.
Por ello Cir1CirNA1Cir es un paralelogramo, y sus diagonales se cortan en el punto medio.
Dado que Cir1A1 es una de esas diagonales, tenemos que la construcción y análisis hecho no depende del vértice de partida, así pues los tres segmentos dados se intersecan en un único punto que es el punto medio entre el circuncentro del triángulo y el centro de la circunferencia de los nueve puntos. Al estar ambos en le recta de Euler, el punto hallado también lo está.
Para ver si está catalogado en

Ricardo Barroso Campos
Didáctica de las Matemáticas
Universidad de Sevilla.