Problema 563.- (Propuesto por Ercole Suppa, profesor titular de matemáticas y física del Liceo Scientifico “A. Einstein”. Teramo, Italia.
Para todos los triángulos de área máxima inscritos en una elipse de ejes 2a y 2b, el área del triangulo pedal del punto de Lemoine es constante e igual a
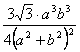
Barisien E. N., Il periodico di Matematica (1911), pag. 40, problema 785.
Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)
A lo largo de la resolución del problema,
utilizaremos la geometría de coordenadas. Partiremos, sin perdida de
generalidad, de la ecuación reducida de la elipse centrada en el origen y no
girada ![]() . Notemos que para evitar confusiones posteriores hemos
cambiado los semiejes de la elipse de las letras latinas a, b, a letras griegas
. Notemos que para evitar confusiones posteriores hemos
cambiado los semiejes de la elipse de las letras latinas a, b, a letras griegas ![]() y
y ![]() . Sea K el punto
simediano del triangulo, también denominado punto de Lemoine o punto de Grebe.
Sin perdida de generalidad supondremos
. Sea K el punto
simediano del triangulo, también denominado punto de Lemoine o punto de Grebe.
Sin perdida de generalidad supondremos ![]() .
.
Un sencillo razonamiento nos conduce
al hecho de que el triangulo de mayor área inscrito en la elipse ha de ser
isósceles (y con base paralela al eje mayor). Sean ![]() ,
, ![]() ,
, ![]() los vértices del triangulo de mayor área inscrito en la
elipse. La expresión para el área del mismo viene dada por
los vértices del triangulo de mayor área inscrito en la
elipse. La expresión para el área del mismo viene dada por
 con
con ![]()
ya que claramente
se deduce que ![]() a partir de la
ecuación de la elipse.
a partir de la
ecuación de la elipse.
Además, también tenemos que para los
valores extremos ![]() ,
, ![]() . Derivando la función
. Derivando la función ![]() que representa el área,
tenemos que
que representa el área,
tenemos que
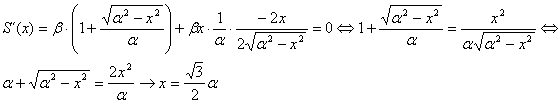
y el valor de la
ordenada correspondiente es entonces ![]() .
.
Podemos ver que 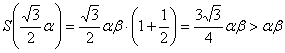 ,
,
y, por lo tanto, ya tenemos el máximo absoluto, y en consecuencia, el triangulo de mayor área. Por otra parte, es fácil observar, utilizando propiedades elementales relacionadas con el baricentro, que el origen de coordenadas del triangulo es precisamente el baricentro de este triangulo de mayor área.
Utilizando conocidas relaciones para la distancia del simediano a los lados de un triangulo, junto con otra conocida relación para el Angulo de Brocard (ya vista en esta revista)
![]() ,
, ![]()
donde ![]() es la distancia del
simediano al lado a, y análogamente para los demás lados del triangulo.
es la distancia del
simediano al lado a, y análogamente para los demás lados del triangulo.
El área del triangulo pedal
originado por el punto de Lemoine se puede determinar sumando las áreas de los
tres triángulos ![]() ,
, ![]() y
y ![]() . De forma particular, el área del triangulo
. De forma particular, el área del triangulo ![]() viene dada por
viene dada por
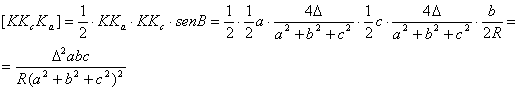
donde a, b, c son los lados del triangulo pedal y además hemos empleado las caracterizaciones ya comentadas junto con el teorema de los senos generalizado. Observemos que el área obtenida es constante, y por simetría sabemos que entonces el área del triangulo pedal pedido será
![]()
en la que hemos
empleado la identidad de Euler ![]() . Por otra parte es muy sencillo determinar las longitudes de
los lados del triangulo de mayor área en función de los valores de los
semiejes, obteniéndose claramente
. Por otra parte es muy sencillo determinar las longitudes de
los lados del triangulo de mayor área en función de los valores de los
semiejes, obteniéndose claramente
![]() ,
, ![]()
y, en consecuencia,
su área será 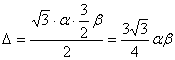 , y para la suma de sus cuadrados
, y para la suma de sus cuadrados 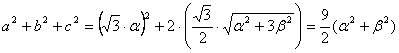
Finalmente,
sustituyendo en la expresión anterior para ![]() , tenemos que
, tenemos que

lo que concluye la demostración.
---oooOooo---