Problema 654
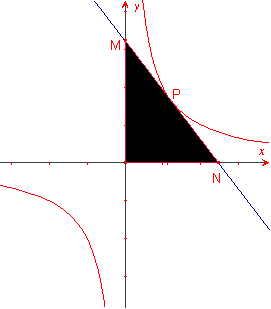
Donada una hipèrbola i un punt de la hipèrbola, l’àrea dels triangles que determinen la intersecció de les rectes tangents a la hipèrbola pel punt i les asímptotes és constant.
 Solució
Ricard Peiró i Estrcuh:
Solució
Ricard Peiró i Estrcuh:
a) Estudiem el cas de la hipèrbola equilàtera:
![]() ,
, ![]()
Siga ![]() un punt de la
hipèrbola. Aleshores,
un punt de la
hipèrbola. Aleshores, ![]()
Les rectes asímptotes són ![]() .
.
La recta tangent a la hipèrbola que passa pel punt P té equació:
![]()
Siga M la intersecció de la recta tangent i l’asímptota ![]()
Les coordenades de M són ![]()
Siga N la intersecció de la recta tangent i l’asímptota ![]()
Les coordenades de N són ![]()
La intersecció de les asímptotes és l’origen de
coordenades ![]()
L’àrea del triangle ![]() és:
és:
![]() .
.
b) Siga la hipèrbola reduïda ![]()
![]()
![]()
Efectuant la transformació lineal:
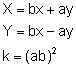 que conserva les
àrees.
que conserva les
àrees.
Ens quedaria l’equació ![]() .
.
Aplicant el apartat a) les àrees dels triangles que determinen la intersecció de les rectes tangents a la hipèrbola per un punt qualsevol de la hipèrbola i les asímptotes és constant i la constant és ab.