Problema 654
Dada una hipérbola y un punto de la hipérbola, el área de los triángulos que determinan la intersección de las rectas tangentes a la hipérbola por el punto y las asíntotas es constante.
Solución de Ricard Peiró:
a) Estudiemos el caso de la hipérbola equilátera:
![]() ,
, ![]()
Sea ![]() un punto de la hipérbola.
Entonces,
un punto de la hipérbola.
Entonces, ![]()
Las
rectas asíntotas son ![]() .
.
La recta tangente a la hipérbola que pasa por el punto P tiene ecuación:
![]()
Sea
M la intersección de la recta tangente y la asíntota ![]()
Las
coordenadas de M son ![]()
Sea
N la intersección de la recta tangente y la asíntota ![]()
Las
coordenadas de N son ![]()
La
intersección de las asíntotas es el origen de coordenadas ![]()
El
área del triángulo ![]() es:
es:
![]() .
.
b)
Sea la hipérbola reducida ![]()
![]()
![]()
Efectuando la transformación lineal:
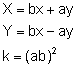 que conserva las áreas.
que conserva las áreas.
Nos
quedaría la ecuación ![]() .
.
Aplicando el apartado a) las áreas de los triángulos que determinan la intersección de las rectas tangentes a la hipérbola por un punto de la hipérbola y las asíntotas es constante, y la constante es ab.