Problema 564.- (Naranjo, J.C.)

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

            A lo largo de la resolución del problema, emplearemos la geometría de coordenadas. Consideraremos, sin perdida de generalidad, que la ecuación de nuestra hipérbola es la siguiente ecuación reducida , con O su centro y donde a y b son los semiejes de la misma. Consideraremos también un punto T de la rama de la hipérbola correspondiente al primer cuadrante de coordenadas .

            Es bien conocido que las ecuaciones de las asintotas de la hipérbola tienen por ecuaciones

                                                   y           

            Por otra parte, derivando implícitamente tenemos . Por tanto, la pendiente de la recta tangente a la rama de la hipérbola en el punto T viene dada por

                                                          

con lo que la ecuación de la recta t, tangente a la hipérbola viene dada por

                                                          

ya que .

            Podemos calcular ahora las coordenadas de los puntos de corte P y Q de la recta tangente a la hipérbola con las rectas asuntotas r y s de la misma. De esta forma

                       

                       

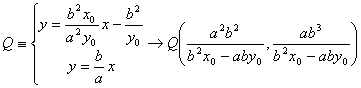
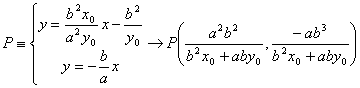
            Podemos, pues, determinar el área del triangulo OQP calculando la altura del mismo (distancia del origen a la recta tangente t) y la base, es decir el modulo del vector QP. De esta forma, tenemos que, después de simplificar

                                  

con lo que para  tenemos

                                       

            Por otra parte, la distancia del centro de la hipérbola a la recta tangente anterior, es bien conocida de la geometría del plano y viene dada por

                                               

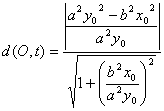
            Finalmente, el área del triangulo OQP  viene dado por

           

que es un valor constante, e independiente del punto T de la hipérbola elegido inicialmente.

                                                           ---oooOooo---