Propuesto por William Rodríguez Chamache. Profesor de geometría de la "Academia integral Trujillo- Perú.

Problema 565

Sea ABCD un cuadrado. Por A se traza cualquier triángulo PAQ con P sobre BC, Q sobre CD y <PAQ=45º. Sean M y N los puntos de intersección de la diagonal BD con AP y AQ. Demostrar que 2(BM BM +ND ND)=PQ PQ.

Rodríguez, W. (2010): Comunicación personal.

Solución del director:

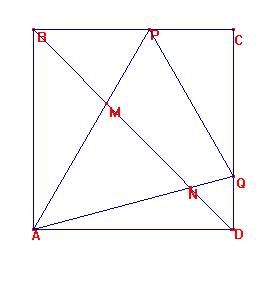
Es <AQD=Q, <ADQ=45º, <QND=135-Q=<ANM, <MAN=45º, <AMN=Q=AQD. Luego AMQD es un cuadrilátero concíclico.

Tracemos la circunferencia circunscrita a AQD. Sea U el punto de corte con AB.

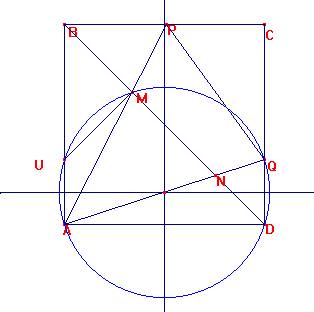
Es <AUQ=180º-<ADQ=180º-90º=90º. Por ser AMQD concíclico, es QUM=QAM=45º. Luego <BUM=180º-<QUA-<BUM=180º-45º-45º, y así, el triángulo BUM es rectángulo e isósceles. Por tanto, .

Similar argumento nos lleva a que  .

Al ser el triángulo PCQ rectángulo se obtiene por fin , cqd.

Ricardo Barroso Campos

Didáctica de las Matemáticas.

Universidad de Sevilla