Problema 565.- (Propuesto por William Rodríguez Chamache, profesor de geometría de la “Academia integral”. Trujillo, Perú.

            Sea ABCD un cuadrado. Por A se traza cualquier PAQ con P sobre BC, Q sobre CD y . Sean M y N los puntos de intersección de la diagonal BD con AP y AQ. Demostrar que .

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

            A lo largo de la resolución del problema utilizaremos la geometría de coordenadas. Sin perdida de generalidad, supondremos que nuestro cuadrado ABCD tiene lado unidad y sus vértices tienen por coordenadas , ,  y . Supondremos también que el punto P genérico tiene por coordenadas  con .

            De esta forma (utilizando la geometría de coordenadas en el plano) es inmediato, determinar las ecuaciones de las rectas ,  y  que son las siguientes

                                                          

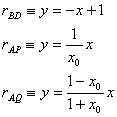
donde, en la ecuación de  hemos empleado la relación bien conocida entre la tangente del ángulo que forman dos rectas (45º en nuestro caso) y sus pendientes respectivas.

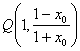            Podemos entonces determinar, a partir de, las coordenadas del punto Q que son , y las de  M y N  resolviendo sistemas de ecuaciones siguientes.

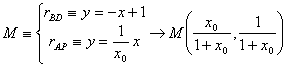
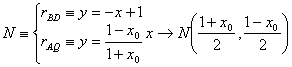
            De esta forma, podemos determinar fácilmente las coordenadas de los vectores

            , ,

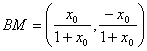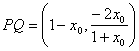
y después de hallar los correspondientes cuadrados de módulos, tenemos que

                       

                       

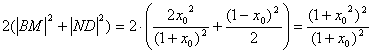
lo que concluye la demostración de la proposición que afirmaba el enunciado del problema.

                                                           ---oooOooo---