Problema 567.- En un triangulo ABC cuyo ángulo C es de 30º, se construye sobre el lado AB hacia el exterior un triangulo equilátero. Demostrar que con los segmentos CA, CB y CD se puede construir un triangulo rectángulo.

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

            A lo largo de la resolución del problema emplearemos la notación habitual en la geometría del triangulo. Aplicando el teorema de los cosenos al triangulo CBD, la conocida expresión para el área del triangulo , y desarrollos trigonométricos elementales, tenemos que

           

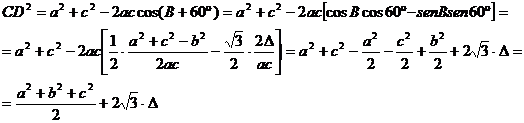
            Por tanto, en virtud del teorema reciproco al de Pitágoras, el problema quedara demostrado si somos capaces de probar la identidad siguiente

         [1]

            Por otra parte, como el ángulo C vale 30º, tenemos que

       

y aplicando el teorema de los cosenos al triangulo ABC, tenemos que

y sustituyendo estas expresiones en [1] vimos que se cumple la identidad

                       

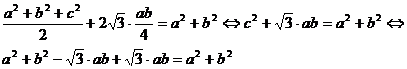
lo que demuestra la proposición.

                                                           ---oooOooo---